1.找到自己电脑公钥C:Users**用户名**.ssh这个目录
id-rsa和id-rsa.pub两个文件, 第一个是私钥文件,第二个是公钥文件

2.将公钥添加到远程linux系统中

sudo vim /root/.ssh/authorized_keys

:wq保存退出

3.启用秘钥方式登录

sudo vim /etc/ssh/sshd_config

PubkeyAuthentication yes的注释去掉

:wq保存退出

4.检查ssh服务

sudo netstat -ntlp | grep ssh 如果有22端口说明已经启动，如果没有列出执行以下命令

/etc/init.d/ssh resart

5.配置vscode远程连接信息

1.vscode安装Remote - SSH

2.Remote Explorer里面选择SSH Targets

3.选择+号添加连接信息， ssh user@ip -p 22, 其中user为远程电脑登录用户名，ip为远程电脑ip地址

如果配置过程中出现 过程试图写入的管道不存在找到以下文件

C:Users**用户名**.sshconfig

``` 右键 属性->安全->高级->禁用继承/然后 添加->->高级->立即查找->选择你的用户名->添加上**修改**的权限`

`` 然后使用vscode再次连接，中间过程会弹出输入登录机器密码的对话框，输入即可

仅作记录

ref: http://t.zoukankan.com/guanglin-p-14931464.html

一、计算机基础

1. C/C++内存有哪几种类型？
   C中，内存分为5个区：堆(malloc)、栈(如局部变量、函数参数)、程序代码区（存放二进制代码）、全局/静态存储区（全局变量、static变量）和常量存储区（常量）。此外，C++中有自由存储区（new）一说。
   全局变量、static变量会初始化为缺省值，而堆和栈上的变量是随机的，不确定的。

2. 堆和栈的区别？
   1).堆存放动态分配的对象——即那些在程序运行时动态分配的对象，比如 new 出来的对象，其生存期由程序控制；
   2).栈用来保存定义在函数内的非static对象，如局部变量，仅在其定义的程序块运行时才存在；
   3).静态内存用来保存static对象，类static数据成员以及定义在任何函数外部的变量，static对象在使用之前分配，程序结束时销毁；
   4).栈和静态内存的对象由编译器自动创建和销毁。

3. 堆和自由存储区的区别？
   总的来说，堆是C语言和操作系统的术语，是操作系统维护的一块动态分配内存；自由存储是C++中通过new与delete动态分配和释放对象的抽象概念。他们并不是完全一样。
   从技术上来说，堆（heap）是C语言和操作系统的术语。堆是操作系统所维护的一块特殊内存，它提供了动态分配的功能，当运行程序调用malloc()时就会从中分配，稍后调用free可把内存交还。而自由存储是C++中通过new和delete动态分配和释放对象的抽象概念，通过new来申请的内存区域可称为自由存储区。基本上，所有的C++编译器默认使用堆来实现自由存储，也即是缺省的全局运算符new和delete也许会按照malloc和free的方式来被实现，这时藉由new运算符分配的对象，说它在堆上也对，说它在自由存储区上也正确。

链表

optimization problem

1. 无约束的优化问题
2. 带等式约束的优化问题
3. 带不等式约束的优化问题

dual

KKT

经典注水问题：
$$
min -\sum^n_{i=1}log(\alpha + x_i) \
s.t.~~~~~~~~ x \geq, 1^Tx=1
$$
其中$\alpha_i >0$ 。

令$x^*$ and $(\lambda^*,v*)$分别是原问题和对偶问题的某对最优解，对偶间隙为0，可以得到如下的KTT条件：
$$
x^* > 0,~~~ 1^Tx^*=1,~~~\lambda^\succeq0,~~~ \lambda_i^x_i^*=0,i=1…n, \
\frac{-1}{\alpha_i + x_i^*}-\lambda_i^*+v^*=0, i=1…,n
$$
$\lambda^*$在最后一个方程里是一个松弛变量，可以消去。
$$
x^* > 0,~~~ 1^Tx^*=1,~~~\lambda^\succeq0,~~~ x_i^(v^* - \frac{1}{\alpha_i + x_i^*})=0,i=1…n, \
v^* \geq \frac{1}{\alpha_i + x_i^*}, i=1…,n
$$
所以有下式：
$$
x_i^*=\left{ \begin{aligned} &\frac{1}{v^*}-\alpha_i, &v^* < \frac{1}{\alpha^*} \
&0 , &v^\geq \frac{1}{\alpha^}
\end{aligned}
\right.
$$
更简洁地，$x^* = max{\frac{1}{v^*} - \alpha_i, 0}$, 将该值代入条件$1^Tx^*=1$，可以得到
$$
\sum^n_{i=1}max{ 0,\frac{1}{v^*}-\alpha_i }=1
$$

单纯形法

单纯形算法适用的情况

标准的线性规划格式
$$
& max~~~ c^Tx \
& ~~~~~~~~~s.t. ~~~A*x \leq b \
&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ x_i \geq 0, i = 1,2,3,…,n
$$
松弛型

主问题是 $2x_1 + x_2$, 不是$x_3$

加入非负松弛变量

单纯形

ref: https://zhuanlan.zhihu.com/p/388224103

影子价格

Row Generation（就是割平面法）

常用于整数规划

割平面方法，从更宏观的角度，可以看作是一种行生成方法。这里的“行”（row），指的是线性不等式。每找到一个cut，就增加一个线性不等式。

线性规划的算法复杂度和连续变量呈多项式级关系，另外随着约束条件（不等式）个数的增加，求解时间也会随之增加。（不确定呈什么关系，求拍砖）

上面说到整数规划的算法复杂度和整数变量的个数n基本呈指数关系，那么它还和其他什么因素相关呢？答案是不等式的个数。（recall求解整数规划需要求解一个个的线性规划）

我们从线性规划角度，理解行生成方法的基本思想：形成极值（最优解）所需要的约束条件个数，往往远小于原问题的约束条件个数。因此为何不在需要的时候，才把这些“重要”的约束条件加上来呢？

下面举个简单例子：

如下图，原问题有5个不等式（一条红线代表一个不等式），但是最优解点D只需CD和DE 2个不等式即可表述。

因此行生成方法的基本思路：先求解原问题的松弛问题，即初始问题（master problem）不加约束条件或只加其中几个约束，然后求解该松弛问题，如果得到的解是可行解，那么该解就是原问题的最优解（例如刚开始运气很好地加了CD和DE）。

如果得到的解对原问题是不可行的，例如解是（0，6）这个点（因为没有加BC这个约束），或者无界的，那么这时候加上BC这个不等式便可以把这个不可行解排除。

以此循环，直到松弛问题的解是可行的，那么该解也是原问题的最优解。

而通过行生成方法，上面问题本来需要5个约束条件，很可能只需要2-3个约束条件，上面的循环已经终止了。

在实际问题中，最优解所需要的约束条件往往远远小于原问题的约束条件个数。例如几万个约束条件，实际只有几百个是用来刻画最优解的。那么这个时候，割平面方法便可以大大提速线性规划的求解。

在上一节的TSP问题中，subtour elimination constraints的个数是指数级的（因此不可能把他们全部加进来），但是求解实际问题中，往往通过割平面方法只需找到其中几千或几百个，即可找到原问题的最优解。用到的，正是相似的思路。

其实TSP问题是有完整刻画的表达式的（Complete Formulation），这时的约束个数虽然不是指数级，但是数量也非常大，因此求解效率很低。割平面方法的引入，大大增加了TSP问题求解的高效性，这也是该方法一次完美的show off。

搜索Literature 行生成方法，最先映入眼帘的可能是Benders’ Decomposition。在那里，一般把整数和实数变量隔离做分解，然后有比较“严格”的如何选取初始约束以及如何一步步地增加约束（feasibility cut和optimality cut）。

与行生成法对偶的方法，是列生成法（逐步增加变量个数）。其中的Dantzig-Wolfe分解法，是Benders’ Decomposition的dual problem。

ref: https://zhuanlan.zhihu.com/p/28387290?group_id=893712252413284352

column generation

列生成算法（Column Generation Algorithm）是一种用于求解大规模线性优化问题的高效算法，本质上来讲，列生成算法是单纯形法的一种形式，用来求解线性规划问题。

列生成算法已被应用于求解很多著名的NP-hard优化问题，如机组人员调度问题（Crew assignment problem）、切割问题（Cutting stock problem）、车辆路径问题（Vehicle routing problem）、单资源工厂选址问题（The single facility location problem）等

基本思想

列生成算法通过求解子问题（sub problem）来找到可以进基的非基变量，该非基变量在模型中并没有显性的写出来（可以看成是生成了一个变量，每个变量其实等价于一列，所以该方法被称为列生成算法）。如果找不到一个可以进基的非基变量，那么就意味着所有的非基变量的检验数（Reduced Cost，RC）都满足最优解的条件，也就是说，该线性规划的最优解已被找到。其思路如下：

1、先把原问题（Master Problem，MP）转换到一个规模更小（即变量数比原问题少）的问题上，这个只使用部分变量的模型被称为原问题的RMP 问题（Restricted Master Problem）。在RMP上用单纯形法求最优解，注意此时求得的最优解只是RMP上的，并不是MP的最优解。

2、然后需要通过一个子问题去检测在那些未被考虑的变量中是否有使得RC小于零的情况，如果有，那么就把这个变量的相关系数列加入到RMP的系数矩阵中，返回第1步。

经过反复迭代，直到子问题中的RC都大于等于零，此时就找到了MP的最优解。

注意min和max问题的影子价格

拉格朗日松弛

拉格朗日对偶（问题）

bender’s decomposition

主要思想是行生成+割平面方法

single bender’s

multi bender’s

branch and bound（精确算法）

分支定界

分支定界算法始终围绕着一颗搜索树进行的，我们将原问题看作搜索树的根节点，从这里出发，分支的含义就是将大的问题分割成小的问题。大问题可以看成是搜索树的父节点，那么从大问题分割出来的小问题就是父节点的子节点了。分支的过程就是不断给树增加子节点的过程。而定界就是在分支的过程中检查子问题的上下界，如果子问题不能产生一比当前最优解还要优的解，那么砍掉这一支。直到所有子问题都不能产生一个更优的解时，算法结束。

例子

对于一个整数规划模型：
$$
maximize~~~~~~&4x_1+9x_2+6x_3 \
subject~ to~~~~&5x_1+8x_2+6x_3 \leq 12 \
&x_1,x_2,x_3 ~ are~ binary~ variable
$$
因为求解的是最大化问题，不妨先设当前的最优解为负无穷：-INF。

1. 首先从主问题分出两支子问题：

通过线性松弛求得两个子问题的upper bound为Z_LP1 = 12.75，Z_LP2 = 12.2。由于Z_LP1 和Z_LP2都大于BestV=-INF，说明这两支均满足要求。继续往下。

2. 从节点 1 和节点 2 两个子问题再次分支，得到如下结果

子问题3已经不可行，无需再理。子问题4通过线性松弛得到最优解为10，刚好也符合原问题0的所有约束，在该支找到一个可行解，更新BestV = 10。

子问题5通过线性松弛得到upper bound为11.87>当前的BestV = 10，因此子问题5还有戏，待下一次分支。而子问题6得到upper bound为9<当前的BestV = 10，那么从该支下去找到的解也不会变得更好，所以剪掉！

3. 对结点5进行分支

子问题7不可行，无需再理。子问题8得到一个满足原问题0所有约束的解，但是目标值为4<当前的BestV=10，所以不更新BestV，同时该支下去也不能得到更好的解了。

4. 此时，所有的分支遍历都完成，我们最终找到了最优解。

分支定界法（branch and bound）是一种求解整数规划问题的最常用算法。这种方法不但可以求解纯整数规划，还可以求解混合整数规划问题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

1. Using a heuristic, find a solution xh to the optimization problem. Store its value, B = f(x_h). (If no heuristic is available, set B to infinity.) B will denote the best solution found so far, and will be used as an upper bound on candidate solutions.

2. Initialize a queue to hold a partial solution with none of the variables of the problem assigned.

3. Loop until the queue is empty:

	3.1. Take a node N off the queue.
	
	3.2. If N represents a single candidate solution x and f(x) < B, then x is the best solution so far. Record it and set B ← f(x).
	
	3.3. Else, branch on N to produce new nodes Ni. For each of these:

		3.3.1. If bound(N_i) > B, do nothing; since the lower bound on this node is greater than the upper bound of the problem, it will never lead to the optimal solution, and can be discarded.
		
		3.3.2. Else, store Ni on the queue.

ref: https://www.cnblogs.com/dengfaheng/p/11225612.html

branch and cut

branch and cut其实还是和branch and bound脱离不了干系的。

在应用branch and bound求解整数规划问题的时候，如下图:

假如，我们现在求一个整数规划最大化问题，在分支定界过程中，求解整数规划模型的LP松弛模型得到的非整数解作为上界，而此前找到的整数解作为下界。 如果出现某个节点upper bound低于现有的lower bound，则可以剪掉该节点。否则，如果不是整数解继续分支。

此外，在求解整数规划模型的LP松弛时，If cutting planes are used to tighten LP relaxations。那么这时候的branch and bound就变成了branch and cut。 割平面

红色部分是整数规划的可行解空间。
蓝色部分是整数规划的LP松弛可行解空间。
在求解LP松弛时，加入橙色的cut，缩小解空间，同时又不影响整数解的解空间，可使解收敛得更快。

这就是branch and cut的过程了。比branch and bound高明之处就在于多了一个cutting planes，可能使branch and bound的效率变得更高。

例子
$$
min~~~~~~~~~~~~~ &z=-6x_1-5_2 \
subject~to~~~&3x_1+x_2 \leq 11 \
&-x_1+2x_2 \leq 5 \
&x_1,x_2 \geq 0
$$

ref: https://www.cnblogs.com/dengfaheng/p/11344488.html

更加详细的一个参考：https://zhuanlan.zhihu.com/p/28387290?group_id=893712252413284352

内点法

各类梯度下降法和牛顿法

批量梯度下降：

1. 是最小化所有样本的损失函数，最终得到全局最优解。　　　　　　

2. 由于每次更新参数需要重新训练一次全部的样本，代价比较大，适用于小规模样本训练的情况。

随机梯度下降：

1. 是最优化每个样本的损失函数。每一次迭代得到的损失函数不是，每次每次向着全局最优的方向，但是大体是向着全局最优，最终的结果往往是在最优解的附近。　　　

2. 当目标函数是凸函数的时候，结果一定是全局最优解。

   　　　　　　　3. 适合大规模样本训练的情况。

小批量梯度下降法：

　将上述两种方法作结合。每次利用一小部分数据更新迭代参数。即样本在1和m之间。

牛顿法：

是通过求解目标函数的一阶导数为0时的参数，进而求出目标函数最小值时的参数。

优点：收敛速度很快。海森矩阵的逆在迭代过程中不断减小，可以起到逐步减小步长的效果。

缺点：海森矩阵的逆计算复杂，代价比较大，因此有了拟牛顿法。

x多变量时，二阶导使用hessian 矩阵

梯度下降法：

是通过梯度方向和步长，直接求解目标函数的最小值时的参数。

越接近最优值时，步长应该不断减小，否则会在最优值附近来回震荡。

使用牛顿法/拟牛顿法收敛更快。但是每次迭代的时间比梯度下降法长。

ref: https://zhuanlan.zhihu.com/p/112416130

CO

MIP

MILP

非线性转为线性

基于CO，CO做了有功和无功的平衡

将约束条件转换为惩罚项。使得主问题变为线性问题，求解MILP

RO

苏文藻课程

SO

苏文藻课程

distributionally robust optimization

苏文藻课程

粒子群算法（PSO）和遗传算法

PSO: partivcle swarm optimizatioin

GA: genetic algorithm

PSO和GA的相同点：

1. 都属于仿生算法。PSO主要模拟鸟类觅食、人类认知等社会行为而提出；GA主要借用生物进化论中”适者生存“的规律。
2. 都属于全局优化方法。两种算法都是在解空间随机产生初始种群，因为算法在全局的解空间进行搜索，且将搜索重点集中在性能高的部分。
3. 都属于随机搜索算法。都是通过随机优化方法更新种群和搜索最优点。PSO中认知项和社会项前都加有随机数。GA的遗传操作均属于随即操作。
4. 都隐含并行性。搜索过程是从问题解的一个集合开始，而不是从单个个体开始，具有隐含并行搜索特性，从而减小了陷入局部极小的可能性。
5. 根据个体的适配信息进行搜索，因此不受函数约束条件的限制，如连续性、可导性等。
6. 对高维复杂问题，往往会遇到早熟收敛和收敛性能差的缺点，都无法保证收敛到最优点。

PSO和GA的不同点：

1. PSO有记忆，好的解的所有粒子均保存，而GA没有记忆，以前的知识随着种群的改变而被破坏。
2. GA算法中，染色体之间相互共享信息，所以整个种群的移动是比较均匀的向最优区域移动。PSO中的例子仅仅通过当前搜索到的最优点进行共享信息，所以很大程度上这是一种单项信息共享机制，整个搜索更新过程是跟随当前最优解的过程。在大多数情况下，所有粒子可能比遗传算法中的进化个体以更快速度收敛于最优解。
3. PSO相对于GA，不需要编码，没有交叉和变异操作，粒子只是通过内部速度进行更新，因此原理更简单、参数更少、实现更容易。
4. PSO算法主要应用于连续问题，包括神经网络训练和函数优化等，而GA除了连续问题之外，还可应用于离散问题，比如TSP问题、货郎担问题、工作车间调度等。

禁忌搜索算法

禁忌搜索(Tabu Search, TS)也是属于模拟人类智能的一种优化算法。

禁忌表（Tabu List，TL）
是用来存放（记忆）禁忌对象的表。它是禁忌搜索得以进行的基本前提。禁忌表本身是有容量限制的，它的大小对存放禁忌对象的个数有影响，会影响算法的性能。

禁忌对象（Tabu Object，TO）
是指禁忌表中被禁的那些变化元素。禁忌对象的选择可以根据具体问题而制定。例如在旅行商问题（Traveling Salesman Problem，TSP）中可以将交换的城市对作为禁忌对象，也可以将总路径长度作为禁忌对象。

禁忌期限（Tabu Tenure，TT）
也叫禁忌长度，指的是禁忌对象不能被选取的周期。禁忌期限过短容易出现循环，跳不出局部最优，长度过长会造成计算时间过长。

渴望准则（Aspiration Criteria，AC）
也称为特赦规则。当所有的对象都被禁忌之后，可以让其中性能最好的被禁忌对象解禁，或者当某个对象解禁会带来目标值的很大改进时，也可以使用特赦规则。

非对称的旅行商问题（ATSP）

分析：这是一个简单的问题,利用枚举的方法也可以找到最优的答案，但是，找到答案不是我们的目的，我们主要是想通过一一个简单的例子来理解禁忌搜索是如何进行工作的。从距离矩阵D可以看到，这是一个非对称的TSP问题，但是这并不影响算法的执行。由于题目假设了邻域构造的方式，而且规定了始点和终点都是城市a，因此，在以下的求解过程中，我们不使用城市a和其他城市进行交换，这样的操作并不会影响全局寻优的能力。

注：在实际应用中，通过选择更高的禁忌对象，设置合理的禁忌期限，或者采用其他更好的的参数，都可以避免循环（反复出现同种情况的邻域值）的出现，提高算法的性能。

常见的机器学习算法

SVM

机器学习给的KKT和凸优化给的不同。但是我认为二者是等价的，应该可以互推。

这个是凸优化上的条件。

贝叶斯

后验概率的获得主要有两种策略

1. 给定x，直接建模$P(c|x)$来预测c，这样叫做”判别式模型“
2. 先对联合概率分布$P(x|c)$建模，然后再由此获得$P(c|x)$.

$$
P(c|x)&= \frac{P(cx)}{P(x)} =\frac{P(c)P(x|c)}{P(x)} \
&=\frac{P(c)}{P(x)}\cdot\frac{P(x|c)}{P(x)}\
&= \frac{P(c)}{P(x)}\cdot \prod_{i=1}^{d}P(x_i|c)
$$

$P(cx) = P(c)P(x|c) = P(x)P(x|c)$

朴素贝叶斯要求独立同分布。

半朴素贝叶斯分类器，对属性条件独立性假设进行了一定程度的放松。

贝叶斯网，借助有向无环图来刻画属性之间的依赖关系。用条件概率表来描述属性的联合概率分布。

EM算法

我们一直假设训练样本的所有属性都被观测到，即训练样本是完整的，但是现实中常遇到不完整的样本，这种未能观测到的特征称为”隐变量“。

令X表示已观测到的变量集，Z表示隐变量集，$\Theta$表示模型参数，若欲对$\Theta$做极大似然估计，则应该最大化对数似然。
$$
LL(\Theta|X,Z) = \ln P(X,Z|\Theta)
$$
由于Z是隐变量，该式无法求解，此时可以通过对Z计算期望，来最大化已观测数据的对数”边际似然“

$\propto$正比于

Linear model

HMM

隐马尔科夫模型是结构最简单的动态贝叶斯网，是一种著名的有向图模型，主要用于时序数据建模，在语音识别、自然语言处理等领域有广泛应用。

三个基本步骤

1. 给定参数，观测序列，计算条件概率

2. 参数学习，给定序列，反推参数

3. 解码。给定参数和观测序列，求最大可能性。

次梯度

支撑超平面的斜率就是次梯度。

最起码是凸函数才能保证任意一点的次梯度存在。

次梯度下降

近端梯度

ref：https://blog.csdn.net/qq_38290475/article/details/81052206

特征工程

PCA

风电数据

构建DRO时候，不同机组的历史数据不同，

LDR变换

pickup and delivery problem with time-windows

求解PDPTW问题的算法包括：列生成算法（column generation）、分支切割（branch-and-cut）、分支切割定价（branch-and-cut-and-price）等精确计算算法，禁忌搜索（tabu search）、模拟退火（simulated annealing algorithm）、基于插入搜索的算法（insertion-based heuristic）、自适应大邻域搜索（adaptive large neighborhood search）、变深度搜索（variable-depth search algorithm）。由于在配送场景下，对算法时效性有极高的要求，上述算法均无法适用于配送场景的问题。在后文中，我们将介绍路径规划的问题模型，以及提出的启发式算法（Two-Stage Fast Heuristic），同时给出了一些仿真结果。

ref: https://segmentfault.com/a/1190000024516742

指派问题(Assignment Problems - AP)

https://blog.csdn.net/qq_38361726/article/details/120738776

车辆路径问题(VRP)

VRP是指一定数量的客户，各自有不同数量的货物需求，配送中心向客户提供货物，由一个车队负责分送货物，组织适当的行车路线，目标是使得客户的需求得到满足，并能在一定的约束下，达到诸如路程最短、成本最小、耗费时间最少等目的。

TSP是VRP问题的特例。

旅行商问题(TSP)

其中约束(3)尽管可被简化但仍使得该问题成为了NP问题，因此基于上述讨论，本文将简单介绍可用于解决TSP的启发式算法。

非对称旅行商问题（ATSP）

非对称旅行商问题（STSP）

凸包算法

Graham scan

链表

从尾到头打印链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

1. 栈
2. insert
3.递归

class Solution {
  public:
    void backtrace(vector<int>& vec, ListNode* p){
        if(p->next){
            backtrace(vec, p->next);
        }
        vec.push_back(p->val);
    }
    
    vector<int> printListFromTailToHead(ListNode* head) {
        vector<int> vec;
        if(head == nullptr){
            return vec;
        }       
        backtrace(vec, head);
        return vec;
    }
};

在vector对象尾部之外的位置插入或删除元素可能很慢，那么结合链表与顺序表的特性可以认为vector对象的元素所使用的数据结构应该是顺序表。

反转链表

1
2
3
4
5
6
7
8
9
10

ListNode* ReverseList(ListNode* pHead) {  //头插法反转
        ListNode* newHead = new ListNode(-1); //新的头节点
        while(pHead != nullptr){
            ListNode* nxt = pHead->next;  //提前保存head的下一个结点，防止赋值后head更改
            pHead->next = newHead->next;
            newHead->next = pHead;
            pHead = nxt;
        }
        return newHead->next;
    }

合并两个排序的链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

ListNode* Merge(ListNode* pHead1, ListNode* pHead2) {
        if(pHead1 == nullptr){
            return pHead2;
        }
        if(pHead2 == nullptr){
            return pHead1;
        }
        // 节省空间就不创建新的链表了，较小的当第一个节点
        ListNode *nh = pHead1->val <= pHead2->val?pHead1:pHead2;
        ListNode *prev = nh; // 尾结点
        ListNode *nxt = nullptr; // temp
        while(pHead1 && pHead2){
            if(pHead1->val <= pHead2->val){
                nxt = pHead1;
                pHead1 = pHead1->next;
            }else{
                nxt = pHead2;
                pHead2 = pHead2->next;
            }
            prev->next = nxt;
            prev = prev->next;
        }
        
        while(pHead1){
            prev->next = pHead1;
            prev = prev->next;
            pHead1 = pHead1->next;
        }
        
        while(pHead2){
            prev->next = pHead2;
            prev = prev->next;
            pHead2 = pHead2->next;
            
        }
        prev->next = nullptr;
        return nh;
    }

复杂链表的复制

每个节点中有节点值，以及两个指针，一个指向下一个节点，另一个特殊指针random指向一个随机节点。对此链表进行深拷贝。

浅拷贝：又称值拷贝，将源对象的值拷贝到目标对象中去，本质上来说源对象和目标对象共用一份实体，只是所引用的变量名不同，地址其实还是相同的。

深拷贝：拷贝的时候先开辟出和源对象大小一样的空间，然后将源对象里的内容拷贝到目标对象中去，这样两个指针就指向了不同的内存位置。并且里面的内容是一样的，这样不但达到了我们想要的目的，还不会出现问题，两个指针先后去调用析构函数，分别释放自己所指向的位置。即为每次增加一个指针，便申请一块新的内存，并让这个指针指向新的内存，深拷贝情况下，不会出现重复释放同一块内存的错误。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

/*
struct RandomListNode {
    int label;
    struct RandomListNode *next, *random;
    RandomListNode(int x) :
            label(x), next(NULL), random(NULL) {
    }
};
*/
class Solution {
public:
    RandomListNode* Clone(RandomListNode* pHead) {
        // 先拷贝原链表
        RandomListNode* pre = new RandomListNode(-1);
        RandomListNode* last = pre, * p = pHead;
        unordered_map<RandomListNode*, RandomListNode*> mp;
        while(p){
            RandomListNode* new_node = new RandomListNode(p->label);
            mp[p] = new_node;  // 旧结点对应的新结点
            last->next = new_node;
            p=p->next;
            last = last->next;
        }
        
        for(auto& [key, value]:mp){
            // key 旧结点    value为新结点
            value->random = key->random == nullptr ? nullptr:mp[key->random];
        }
        return pre->next;
    }
};

排序的循环链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57

/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* next;

    Node() {}

    Node(int _val) {
        val = _val;
        next = NULL;
    }

    Node(int _val, Node* _next) {
        val = _val;
        next = _next;
    }
};
*/

class Solution {
public:
    Node* insert(Node* head, int insertVal) {
        Node* node = new Node(insertVal);
        if(head == nullptr){
            node->next = node;
            return node;
        }
        // 1个
        if(head->next == head){
            head->next = node;
            node->next = head;
            return head;
        }
        Node* cur = head;
        Node* nxt = head->next;
        while(nxt!=head){
            if(insertVal>=cur->val && insertVal <= nxt->val){  //  正常递增
                break;
            }
            if(cur->val > nxt->val){  // nxt已经到了最小元素
                if(insertVal > cur->val || insertVal < nxt->val){
                    // insertVal > cur->val 说明 insertval是最大值  3 5 1  插入值为6  结果为 3561
                    // insertVal < nxt->val 说明 insertval是最小值  3 5 1  插入值为0  结果为 3501
                    // 这两种情况都可以插入在 5 和 1 之间
                    break;
                }
            }
            cur = nxt;
            nxt = nxt->next;
        }
        cur->next = node;
        node->next = nxt;
        return head;
    }
};

树

树的子结构

判断一棵树是不是另一棵树的子结构.

没啥好解释的，我直接暴力穷举。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

class Solution {
public:
    bool HasSubtree(TreeNode* pRoot1, TreeNode* pRoot2) {
        if(!pRoot1 || !pRoot2){
            return false;
        }
        
        std::function<bool(TreeNode*, TreeNode*)> compareVal = [&](TreeNode* p, TreeNode* q)->bool{
            if(q == nullptr){
                return true;
            }
           
            if(p == nullptr || p->val != q->val){
                return false;
            }
            return compareVal(p->left, q->left) && compareVal(p->right,q->right);
        };
        bool tag = false;
        queue<TreeNode*> que;
        que.push(pRoot1);
        while(!que.empty()){
            auto temp = que.front();
            que.pop();
            tag = compareVal(temp, pRoot2);
            if(tag){
                return true;
            }
            if(temp->left){
                que.push(temp->left);
            }
            if(temp->right){
                que.push(temp->right);
            }
        }
        return false;
    }
};

二叉树的镜像

我第一反应想的是层次遍历倒序

发现前序，中序获得，倒序构建貌似也可以。没实验过

递归操作也可以用

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

TreeNode* Mirror(TreeNode* pRoot) {   // 递归
        if(pRoot == nullptr){
            return nullptr;
        }
        if(!pRoot->left && !pRoot->right){
            return pRoot;  // 单节点返回自身, {1} return 1;
        }
        TreeNode* temp = pRoot->left;
        pRoot->left = pRoot->right;
        pRoot->right = temp;
        Mirror(pRoot->left);
        Mirror(pRoot->right);
        
        return pRoot;
    }

对称的二叉树

判断二叉树是否对称。

中序遍历拆开 或者 不拆开直接判断，即递归，一样的。

非递归方法，使用stack，每次成双取出，判断p1->left == p2->right && p1->right == p2->left。然后成双放入。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

bool isSymmetrical(TreeNode* pRoot) {
        if(pRoot == nullptr || (!pRoot->left && !pRoot->right)){
            return true;
        }
        
        std::function<bool(TreeNode*, TreeNode*)> cpr = [&](TreeNode* leftt, TreeNode* rightt)->bool{
            if(leftt == nullptr && rightt == nullptr){
                return true;
            }
            // 说明不全空
            if(leftt==nullptr || rightt == nullptr){
                return false;  //一空一不空
            }
            return leftt->val == rightt->val
                   && cpr(leftt->right, rightt->left)
                   && cpr(leftt->left, rightt->right);
        };
        
        return cpr(pRoot->left, pRoot->right);
    }

边界条件处我犯了错。状态判断不好。

从上往下打印二叉树

层次遍历。不赘述

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21

vector<int> PrintFromTopToBottom(TreeNode* root) {
        vector<int> ans;
        if(root == nullptr){
            return ans;
        }
        queue<TreeNode*> que;
        que.push(root);
        while(!que.empty()){
            TreeNode* temp = que.front();
            ans.push_back(temp->val);
            que.pop();
            if(temp->left){
                que.push(temp->left);
            }
            if(temp->right){
                que.push(temp->right);
            }
            
        }
        return ans;
    }

二叉搜索树的后序遍历序列

二叉搜索树的中序遍历是递增的。

后序遍历的最后一位是根节点root

说明序列中，小于root->val的都是左子树，大于的都是右子树

接下来，相似的操作。

如 2 4 3 6 8 7 5 -> root = 5 left: 2 4 3 right: 6 8 7

2 4 3 -> root=3 left = 2 right = 4 6 8 7 -> root = 7 left = 6 right = 8

递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

bool VerifySquenceOfBST(vector<int> sequence) {
       std::function<bool(vector<int>&, size_t, size_t)> judge = 
           [&](vector<int>& seq, size_t l, size_t r)->bool{
           if(l >= r){
               return true;
           }
           int temp = seq[r];  // root
           int i = r - 1;
           while(i>l && seq[i]>temp){
               --i;
           }
           //找到分界点了
           // 判断左侧是否全部都是小于temp的
           for(size_t j = l;j<i;++j){
               if(seq[j]>temp){
                   return false;
               }
           }
           
           return judge(seq, l, i) && judge(seq, i+1, r-1);
       };
        if(sequence.empty()){
            return false;
        }
        size_t n = sequence.size();
        return judge(sequence, 0, n-1);
        
    }

二叉树中和为某一值的路径(二)

找出二叉树中结点值的和为目标值的所有路径（路径指根节点到叶子）

可以及时剪枝。

先序遍历的做法来遍历。

考虑负数！负数的话，大于的判断符号就没法使用

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

class Solution {
private:
    int expect;    
public:
    vector<vector<int>> FindPath(TreeNode* root,int expectNumber) {
        vector<vector<int>> ans;
        if(root == nullptr){
            return ans;
        }
        this->expect = expectNumber;
        
        std::function<void(TreeNode*, int, vector<int>, vector<vector<int>>&)> dfs = 
            [&](TreeNode* rt, int sum,vector<int> temp, vector<vector<int>>& ans) -> void{
            if(rt == nullptr){
                return;
            }
            sum+=rt->val;
            temp.push_back(rt->val);
            if(sum == expect && rt->left == nullptr && rt->right == nullptr){
                ans.push_back(temp);
                temp.clear();
                return;
            }
            // <
            if(rt->left)
                dfs(rt->left, sum, temp, ans);
            if(rt->right)
                dfs(rt->right, sum, temp, ans);
            temp.pop_back();
        };
        
        vector<int> temp;
        dfs(root, 0, temp, ans);
        return ans;
    }
};

二叉搜索树与双向链表

输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向链表。

方法一：直接中序重新构造

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39

/*
struct TreeNode {
	int val;
	struct TreeNode *left;
	struct TreeNode *right;
	TreeNode(int x) :
			val(x), left(NULL), right(NULL) {
	}
};*/
class Solution {
public:
    TreeNode* Convert(TreeNode* pRootOfTree) {
        if(pRootOfTree == nullptr){
            return pRootOfTree;
        }
        std::function<void(TreeNode*, TreeNode*&)> trans = [&](TreeNode* root, TreeNode*& last)->void{
            if(root == nullptr){
                return;
            }
            if(root->left){
                trans(root->left, last);
            }
            last->right = root;
            root->left = last;
            last = root;
            if(root->right){
                trans(root->right, last);
            }
            return;
        };
        
        TreeNode* p = new TreeNode(-1);
        TreeNode* q = p;
        trans(pRootOfTree, q);
        p=p->right;
        p->left = nullptr;
        return p;
    }
};

方法二：不开辟新的结点，直接在原节点操作。这就需要保存中序遍历过程中的前继结点。给个全局变量，保存前继。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41

/*
struct TreeNode {
	int val;
	struct TreeNode *left;
	struct TreeNode *right;
	TreeNode(int x) :
			val(x), left(NULL), right(NULL) {
	}
};*/
class Solution {
public:
    TreeNode* preNode;  // 前驱结点
    TreeNode* Convert(TreeNode* pRootOfTree) {
        // 先找到preNode
        if(pRootOfTree == nullptr){
            return pRootOfTree;
        }
        
        std::function<void(TreeNode*)> trans = [&](TreeNode* root)->void{
            if(root == nullptr) {
            return;
        }
        trans(root->left);  //走到起始点
            // 找到最左侧，此时root == p
        root->left = preNode;
        preNode->right = root;
        preNode = root;    
        trans(root->right);
        };

        TreeNode* p = pRootOfTree;
        while(p->left){
            p = p->left;  // 链表的起始节点
        }
        preNode = new TreeNode(-1);
        trans(pRootOfTree);
        p->left = nullptr;
        return p;  // 链表的头
    }

};

序列化二叉树

请实现两个函数，分别用来序列化和反序列化二叉树，不对序列化之后的字符串进行约束，但要求能够根据序列化之后的字符串重新构造出一棵与原二叉树相同的树。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90

class Codec {
public:
	struct TreeNode {
		int val;
		TreeNode* left;
		TreeNode* right;
		TreeNode(int x) : val(x), left(NULL), right(NULL) {}
	};

	// Encodes a tree to a single string.
	string serialize(TreeNode* root) {
		string res = "";
		TreeNode* p = root;
		preOrder(p, res);
		// 使用递归，把最后一个逗号删除
		res.pop_back();

		// 使用迭代，最后还少个"X"
		// preOrder_case2(p, res);
		// res += "X";

		return res;
	}

	// 使用递归方式
	void preOrder(TreeNode* root, string& str) {
		if (root == nullptr) {
			str += "X";
			str += ",";
			return;
		}
		str += to_string(root->val);
		str += ",";
		preOrder(root->left, str);
		preOrder(root->right, str);
	}

	// 使用 非递归方式 进行前序遍历
	void preOrder_case2(TreeNode* root, string& str) {
		stack<TreeNode*> st;
		st.push(root);
		str = str + to_string(root->left->val) + ",";
		TreeNode* temp = root;
		int visited_node = 0;
		while (temp!= nullptr || !st.empty()) {
			if (temp!=nullptr) {  // 一直向左走
				st.push(temp);
				str += to_string(temp->val);   // 不断保存经过的结点
				str += ",";
				temp = temp->left;  // 走到最左
			}
			else { // 找右子树
				str += "X";   // 不断保存经过的结点
				str += ",";
				temp = st.top();  // 回溯到父结点
				st.pop();
				temp = temp->right;
				
			}
		}
	}


	// Decodes your encoded data to tree.
	TreeNode* deserialize(string data) {  // 只给了一个string ，说明不能通过 前/中 + 后序  来确定唯一的二叉树
		deque<string> que;
		stringstream ss;
		string temp;
		ss << data;
		while (getline(ss, temp, ',')) {
			que.push_back(temp);
		}
		// 按照 ’,‘ 分割好了
		return anls(que);
	}

	// 从左到右解析字符串
	TreeNode* anls(deque<string>& que) {
		// que 从前往后
		if (!que.empty() && que.front() == "X") {  // 为空结点
			que.pop_front();
			return nullptr;
		}
		auto temp = new TreeNode(stoi(que.front()));
		que.pop_front();
		temp->left = anls(que);
		temp->right = anls(que);
		return temp;
	}
};

删除二叉搜索树中的节点

leetcode450

难点主要在于删除操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48

class Solution {
public:
    // cur的左右节点都为空，cur可以直接删除
    // 右节点为空，找左节点的最大值
    // 左节点为空，找右节点的最小值
    // 左右节点均不为空，那么去左边找最大值或右边找最小值都可以,来替换掉cur
    // 解法可以看作不断地重构二叉搜索树(BST)
    TreeNode* deleteNode(TreeNode* root, int key) {
        if(root == nullptr){
            return nullptr;
        }
        if(root->val < key){
            root->right = deleteNode(root->right, key);
            return root;
        }
        if(root->val> key){
            root->left = deleteNode(root->left,key);
            return root;
        }
        if(root->val==key){  // ==
            if(root->left == nullptr && root->right == nullptr){
                // 直接删除root
                return nullptr;
            }
            if(root->right == nullptr){  // 右空，找左边最大值,刚好是左边第一个
                return root->left;
            }
            if(root->left == nullptr){ // 左空，找右边最小值，刚好是右边第一个
                return root->right;
            }
            // 两侧都不为空
            // 这里找右边最小值，换掉root
            TreeNode* rep = root->right;
            // 如果右边第一个有左子树，那么就一直找,因为最小值如果在左子树，那么肯定在第一个结点的左子树
            while(rep->left!=nullptr){
                rep = rep->left;
            }
            // 此时已经找到最小值的结点了
            // 重构需要删除结点的右子树， 值要根据rep（即替换节点的值重构
            root->right = deleteNode(root->right, rep->val);
            // 把这个结点替换掉需要删除的结点 root
            rep->right = root->right;
            rep->left = root->left;
            return rep;
        }
        return root;
    }
};

排序

最小的K个数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

// 长度为 n 的可能有重复值的数组，找出其中不去重的最小的 k 个数
// [0,1,2,1,2],3    ->   [0,1,1]
/*
* case1  直接排序取前K
* case2  容量为K的优先队列(大顶堆)。 小于则进去且弹出堆顶
* case3  topK算法
*/

// case1略


// case2

（大顶）堆的建立，插入，删除

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88

class HeapBID {
public:
	// 数组下标从0开始
	void shiftDown(vector<int>& nums, int k) {  // 向下调整
		int leftChild = k * 2 + 1, rightChild = k * 2 + 2;
		int maxIndex = k; //假设在当前节点，及其左、右子节点，共三个节点中，最大的是当前这个节点。后序我们就要更新max，看到底哪个才是最大的，把最大的那个和当前节点交换
		if (leftChild < nums.size() && nums[leftChild] > nums[maxIndex])
			maxIndex = leftChild;
		if (rightChild < nums.size() && nums[rightChild] > nums[maxIndex])
			maxIndex = rightChild;
		if (maxIndex != k)
		{
			swap(nums[maxIndex], nums[k]);
			shiftDown(nums, maxIndex); // 如果原k节点调整了位置(上一步swap调整)，那么就要将k继续做shiftDown操作，直到它比它的左、右孩子都大
		}
		
	}
	//  建立的是大顶堆
	// 向上调整，删除堆顶时候使用
	void shiftUp(vector<int>& nums) {  // 向上调整
		// 首先将最后一个孩子节点插入到头节点
		int child = nums.size() - 1;
		int parent = (child - 1) / 2;
		while (child > 0) {
			if (nums[parent] < nums[child]) {
				swap(nums[parent], nums[child]);
			}
			else {
				break;
			}
			child = parent;
			parent = (child - 1) / 2;  // 换层
		}
	}

	void buildMaxHeap(vector<int>& nums) {
		int n = nums.size();
		for (int i = 0; i < n/2; ++i) {  // 从第一个非叶子节点开始，从下往上，将每棵子树调整成最大堆
			shiftDown(nums, i);
		}
	}

	void inHeap(vector<int>& nums, int x) {
		nums.push_back(x);
		shiftUp(nums);
	}

	void pollHeap(vector<int>& nums) {
		int oldVal = nums[0]; // 头元素
		nums[0] = nums[nums.size() - 1];
		nums.pop_back(); // 弹出末尾
		shiftDown(nums, 0);
	}
};


/**/
int main() {
	vector<int> nums{ 1,4,9,7,2,6,8 };
	HeapBID h;
	h.buildMaxHeap(nums);
	cout << "build heap" << endl;
	for (auto& a : nums) {
		cout << a << " ";
	}
	cout << endl;
	cout << "insert" << endl;
	h.inHeap(nums,5);
	for (auto& a : nums) {
		cout << a << " ";
	}

	cout << endl;
	cout << "pop " << nums[0] << endl;
	h.pollHeap(nums);
	for (auto& a : nums) {
		cout << a << " ";
	}

	cout << endl;
	cout << "pop all" << endl;
	int n = nums.size();
	for (int i = 0; i < n; ++i) {
		cout << nums[0] << " ";
		h.pollHeap(nums);
	}
	return 0;
}

位运算

模拟

顺时针打印矩阵

从外向里以顺时针打印。

螺旋输出，小心单行的情况，要判断 if (top != bottom) 和 if (left != right)

在这里犯了错。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37

vector<int> printMatrix(vector<vector<int> > matrix) {
        int m = matrix.size();
        int n = matrix[0].size();
        vector<int> ans;
        int left = 0, right = n-1;
        int top = 0, bottom = m-1;
        
        while(left<=right && top<=bottom){
            // 左到右
            for(int i = left;i<=right;++i){
                ans.push_back(matrix[top][i]);
            }
            //上到下
            for(int i = top+1;i<=bottom;++i){
                ans.push_back(matrix[i][right]);
            }
            
            // 小心单行的情况
            //右到左
            if (top != bottom){
                for(int i = right-1; i>=left;--i){
                    ans.push_back(matrix[bottom][i]);
                }
            }
            // 下到上
            if (left != right){
                for(int i = bottom-1;i>top;--i){
                    ans.push_back(matrix[i][left]);
                }
            }
            top++;
            bottom--;
            left++;
            right--;
        }
        return ans;
    }

队列&栈

包含min函数的栈

用了个辅助栈，保存当前最小值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

class Solution {
public:
    stack<int> st;
    stack<int> aux_st;
    void push(int value) {
        st.push(value);
        if(aux_st.empty() || aux_st.top() >= value){
            aux_st.push(value);   //保存当前最小值
        }
    }
    void pop() {
        int temp = st.top();
        st.pop();
        if(temp == aux_st.top()){
            aux_st.pop();
        }
    }
    int top() {
        return st.top();
    }
    int min() {
        return aux_st.top();
    }
};

栈的压入、弹出序列

判断出栈序列有没有可能是入栈序列的对应序列。

入栈1,2,3,4,5

出栈4,5,3,2,1

首先1入辅助栈，此时栈顶1≠4，继续入栈2

此时栈顶2≠4，继续入栈3

此时栈顶3≠4，继续入栈4

此时栈顶4＝4，出栈4，弹出序列向后一位，此时为5，,辅助栈里面是1,2,3

此时栈顶3≠5，继续入栈5

此时栈顶5=5，出栈5,弹出序列向后一位，此时为3，,辅助栈里面是1,2,3

….

依次执行，最后辅助栈为空。如果不为空说明弹出序列不是该栈的弹出顺序

1
2
3
4
5
6
7
8
9
10
11
12
13
14

bool IsPopOrder(vector<int> pushV,vector<int> popV) {
        stack<int> aux_st;
        size_t n = pushV.size();
        size_t j = 0;
        for(size_t i = 0;i < n;++i){
            aux_st.push(pushV[i]);  // 当前值入辅助栈
            while((!aux_st.empty() && aux_st.top()==popV[j])){
                // 判断辅助栈当前顶部能否弹出和当前出栈序列对应的值
                aux_st.pop();
                ++j;  // 出栈序列后移一位
            }           
        }
        return aux_st.empty();
    }

搜索算法

字符串的排列

算法

字符串的排列

tag: 字符串 递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68

vector<string> Permutation(string str) {
        vector<string> vec;
        do{
            vec.push_back(str);
        }while(next_permutation(str.begin(), str.end()));
        return vec;
    }

// string内没有重复字母
class Solution {
public:
    vector<string> ans;
    void permu_unique(string& str, int index){
        if(index == str.size()){
            ans.emplace_back(str);
        }
        for(int i = index;i<str.size();++i){
            swap(str[i], str[index]);
            permu_unique(str, index + 1);
            swap(str[i], str[index]);
        }
    }
    vector<string> Permutation(string str) {
        permu_unique(str, 0);
        return ans;
    }
};

// string内有重复字母
class Solution {
public:
    vector<string> ans;
    vector<int> visited; // 记录重复字母
    
    // index代表选择的字母个数
    void permu(string& str, int index, string& temp){
        if(index == str.size()){
            ans.emplace_back(temp);
        }
        for(int i = 0; i<str.size();++i){
            if(visited[i] || (i>0 && !visited[i-1] && str[i-1] == str[i])){
                //!visited[i-1] && str[i-1] == str[i]
                //这句代表，前一个是没访问过的状态，并且当前字母等于前一个字母
                // 说明  前一个字母已经遍历完了，把状态重置为0，才来这个字母
                // 而两个字母相同，所以不该对当前字母再进行搜索
                continue;
            }
            // 选当前
            temp.push_back(str[i]);
            // 标记为已用
            visited[i] = 1;
            permu(str, index+1, temp);
            // 回退
            temp.pop_back();
            visited[i]=0;
        }
    }
    
    vector<string> Permutation(string str) {
        sort(str.begin(),str.end());
        string temp = "";
        visited.resize(str.size(),0);
        permu(str, 0, temp);
        return ans;
    }
};

其他算法

数组中出现次数超过一半的数字

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

//  题目输入保证有解，不需要在进行验证
int MoreThanHalfNum_Solution(vector<int> numbers) {
        int cnt = 0;
        int num = -1;
        for(auto &a : numbers){
            if(cnt == 0){  // 还没选数字
                num  = a;
                ++cnt;
            }else{
                if(a == num){  // 相同则给当前数字投一票
                    ++cnt;
                }else{
                    --cnt;  // 不同则减去一票
                }
            }
        }
        return num;
    }

分组交换网中的时延、丢包和吞吐量

时延概述

结点处理时延：如检查比特级别的差错所需要二时间，该差错出现在从上游结点向下级路由器传输这些分组比特的过程中。

排队时延：等待进入传输队列的时间。

传输时延：数据块从结点进入传播媒体的时间。

传播时延：从链路的起点到路由器所需要的时间。

排队时延和丢包

排队时延的大小取决于流量是周期性到达还是以突发形式到达

端到端时延

$$
d_{end-end} = N(d_{proc} + d_{trans} + d_{prop})
$$

无拥塞的情况下，没有排队时延。处理时延为proc， 传播时延为prop，trans为传输时延

计算机网络中的吞吐量

瞬时吞吐量

平均吞吐量

计算机网络体系结构和参考模型

计算机网络分层结构

在计算机网络体系结构的各个层次中，每个报文都分为两部分：一是数据部分，即SDU（service Data Unit）服务数据单元；二是控制信息部分，即PCI（Protocol Control Information）。它们共同组成PDU（Protocol Data Unit）协议数据单元，PDU是对等层次之间传递的数据单位。

物理层的PDU称为比特

数据链路层的PDU称为帧

网络层的PDU称为分组

传输层的PDU称为报文

计算机网络协议、接口、服务的概念

协议就是规则的集合

接口是同一结点内相邻两层间交换信息的连接点，每层只能为紧邻的层次之间定义接口。

五层因特网协议栈

应用层：

​ 协议：HTTP, SMTP, FTP

​ 信息分组：报文

运输层：

​ 协议：两个运输协议：TCP、UDP

​ 信息分组：报文段

网络层：

​ 因特网的网络层负责将称为数据报的网络层分组从一台主机转移到另一台主机。

​ 协议：IP协议

​ 信息分组：数据报

数据链路层：

​ 由链路层提供的服务取决于该链路的特定链路层协议。因为数据报从源到目的地传送通常要经过几条链路，一个数据报可能被沿途不同链路上的不同链路层协议处理。

​ 协议：每个链路有自己特定的协议

​ 信息分组：帧

物理层

​ 虽然链路层的任务是将一个个帧从一个网络元素移动到下一个网络元素，而物理层的任务是将该帧中的一个个比特从一个结点移动到下一个结点。

​ 协议：这层的协议仍然是链路相关的，并且进一步与该链路的实际传输媒体相关。例如以太网具有许多物理层协议：关于双绞铜线、关于同轴电缆、关于光纤等。

七层ISO/OSI模型

物理层

传输单位：比特

任务：传输比特流（二进制传输）

功能：在物理媒体上为数据端设备透明传输原始比特流。

主要协议：IEEE802.3

数据链路层

传输单位：帧

任务：将网络层传来的IP数据报组装成帧。

功能：成帧、差错控制、流量控制和传输管理等。

主要协议：MAC 、VLAN、PPP

网络层

传输单位：数据报

任务：把网络层的（PDU）协议数据单元（分组）从源端传到目的端。

功能：流量控制、拥塞控制、差错控制和网际互连等功能。

主要协议：IP、IPX、ICMP（Internet Control Message Protocol）、ARP（Address Resolution Protocol）

因特网的主要协议是无连接的网际协议（IP， internet Protocol）和许多路由选择协议，因此因特网的网络层也叫网际层和IP层

传输层

传输单位：报文段（TCP报文）或数据用户报（UDP）

任务：负责主机中两个进程之间的通信

功能：为端到端提供可靠的传输服务，为端到端提供流量控制、差错控制、服务质量、数据传输管理等服务。

主要协议：TCP、UDP

会话层

传输单位：会话层协议数据单元（Session Protocol Data Unit, SPDU）

任务：允许不同主机上的各个进程之间进行会话。会话也称建立同步（synchronize）

功能：负责管理主机间的会话进程，包括建立、管理及终止进程间的会话

主要协议：RPC（远程调用协议 Remote Procedure Call Protocol）、NFS（Network File System）

表现层

传输单位：PPDU（Presentation Protocol Data Unit 表示协议数据单元）

功能：对数据进行翻译、加密和压缩

主要协议：ASCII、JPEG

应用层

传输单位：APDU（Application Protocol Data Unit 应用协议数据单元）

功能：允许访问OSI环境的手段

主要协议：FTP、HTTP、DNS

TCP/IP模型

TCP/IP模型与OSI参考模型的比较

• 相似之处

  • 二者都采用分层体系结构，将庞大且复杂的问题划分为若干较容易处理的、范围较小的问题。
  • 二者都是基于独立的协议栈的概念。
    • 协议栈（英语：Protocol stack），又称协议堆叠，是计算机网络协议套件的一个具体的软件实现。协议套件中的一个协议通常是只为一个目的而设计的，这样可以使得设计更容易。因为每个协议模块通常都要和上下两个其他协议模块通信，它们通常可以想象成是协议栈中的层。
  • 二者都可以解决异构网络的互联，实现不同计算机之间的通信。

• 不同之处

  • OSI参考模型的最大贡献就是精确地定义了三个主要概念：服务、协议和接口，这与面向对象的设计思想非常吻合。而TCP/IP模型在这三个概念上没有明确的区分。
  • OSI参考模型在协议发明之前，没有偏向于任何特定的协议，通用性良好。TCP/IP模型在设计方面最先出现的是协议，模型实际上是对已有协议的描述，因此不会出现协议不匹配模型的情况，但是模型不适合于非TCP/IP模型。
  • TCP/IP模型在设计之初就考虑到了多种异构网的互联问题，并把IP作为一个单独的重要层次。
  • OSI参考模型在网络层支持无连接和面向连接的通信，而在传输层仅又面向连接的通信。而TCP/IP模型认为可靠性是端到端的问题，因此它在网际层仅有一种无连接的通信模式，但传输层支持无连接和面向连接的通信模式。

物理层

数据链路层

网络层

传输层

应用层

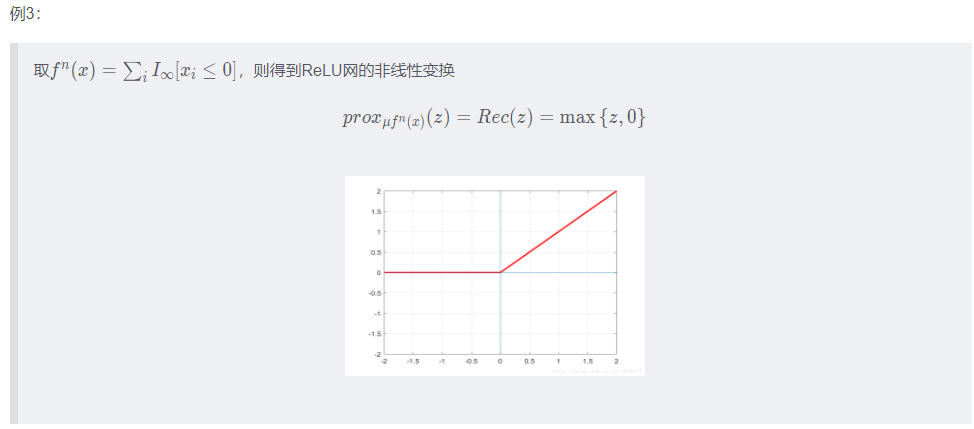
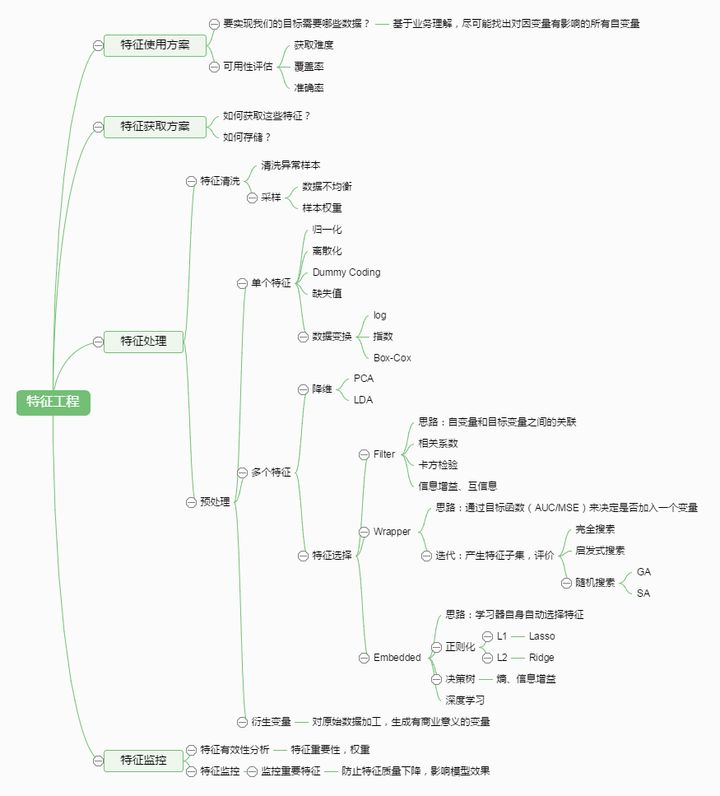
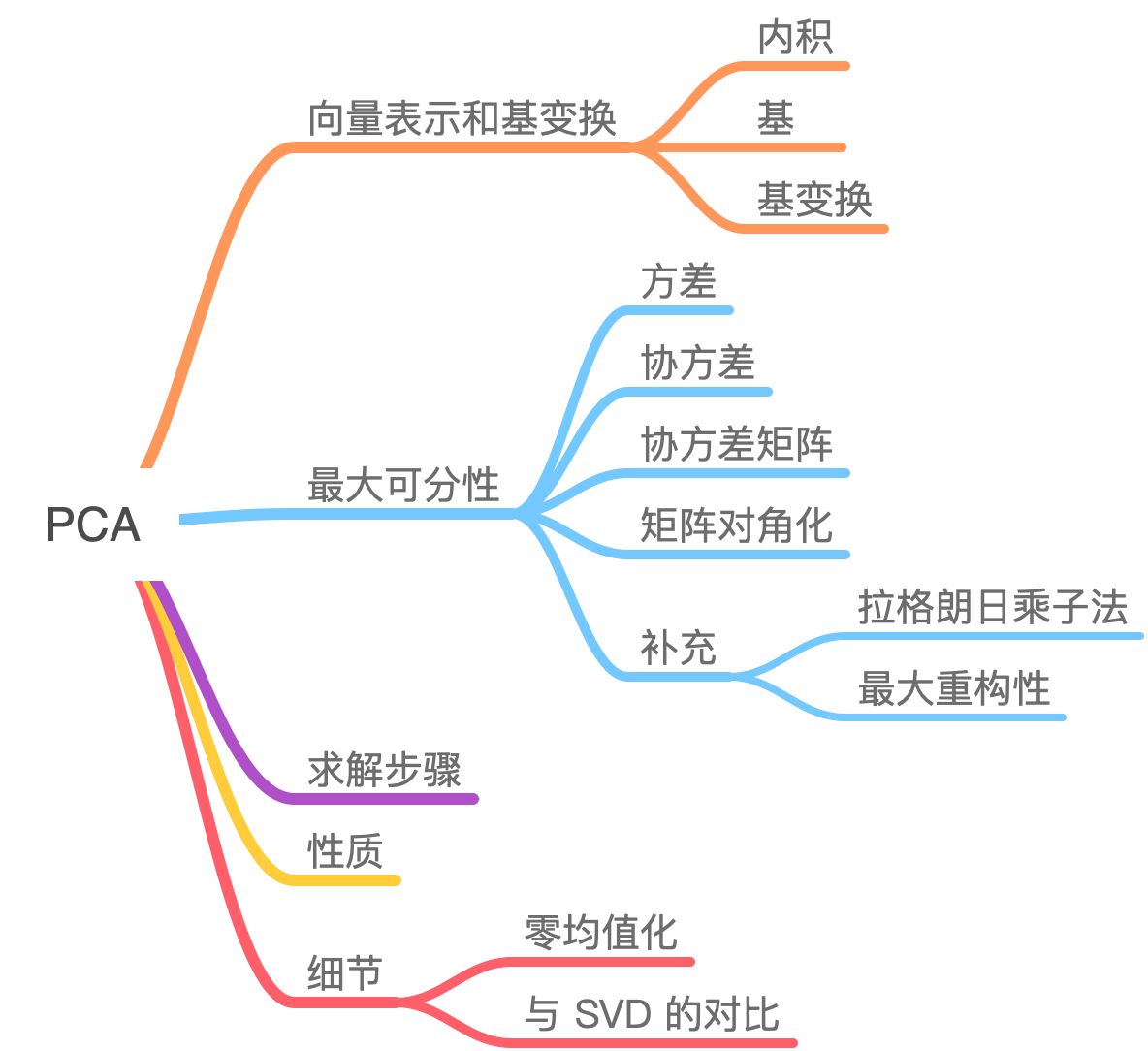
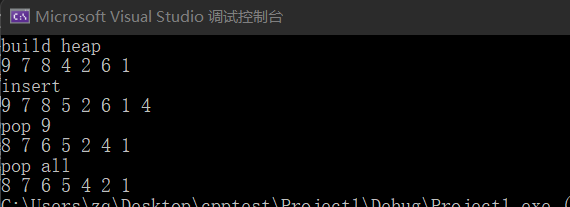
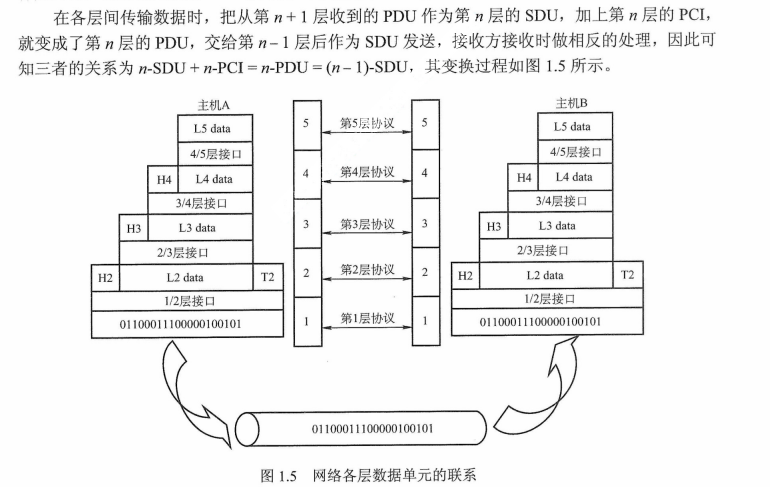
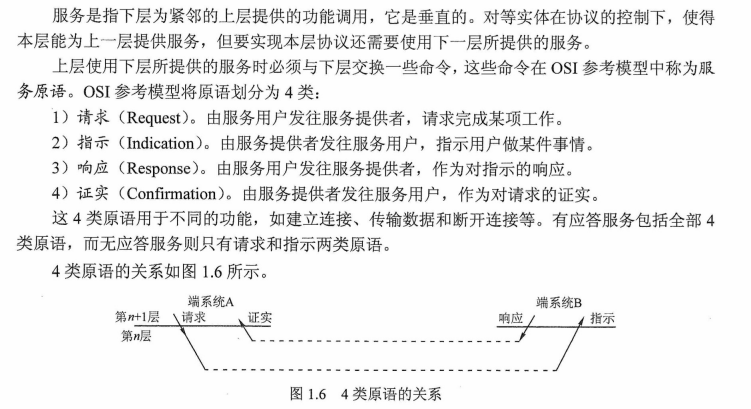
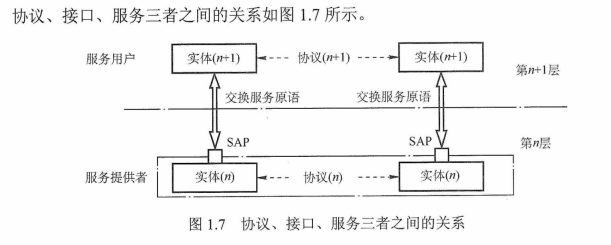
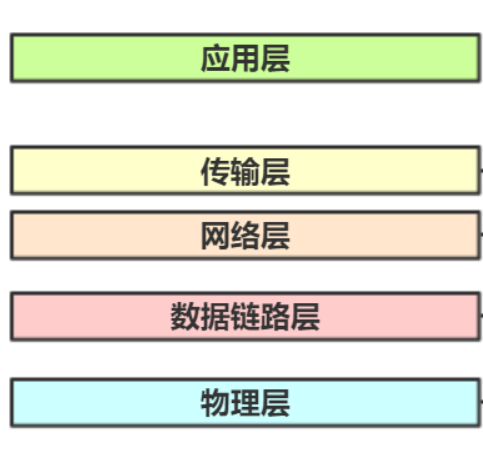
操作系统实验

操作系统概览

什么是操作系统

用户角度： 操作系统是一个 控制软件：

• 管理应用程序。
• 为应用程序提供服务。
• 杀死应用程序。

对内角度： 操作系统用于资源管理：

• 管理外设、分配资源。

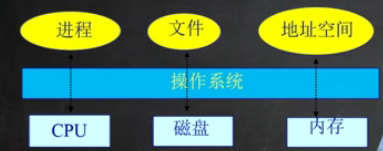
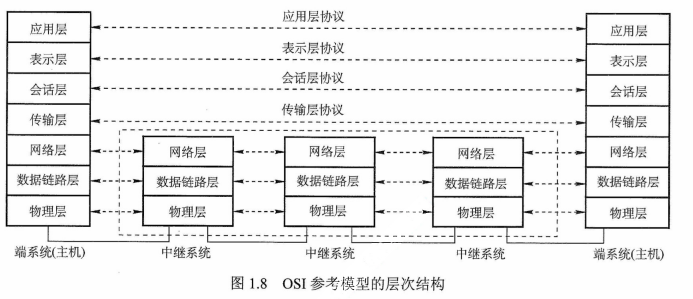
操作系统是硬件之上、应用程序之下的层次结构。
操作系统位于应用软件之下，为应用软件提供服务支撑。

外壳（shell） 内核（kernel）。

内核空间是操作系统内核访问的区域，独立于普通的应用程序，是受保护的内存空间。

用户空间是普通应用程序可访问的内存区域。

操作系统包含什么

硬件资源三大块：CPU、内存、磁盘。

CPU： CPU调度、进程线程。
内存： 物理内存管理、虚拟内存管理（在有限物理内存之上为应用提供内存）。MMU
文件系统： disk过于底层，不方便上层应用。所以我们做出文件系统管理。
中断处理与设备驱动： 驱动实现操作系统。

OS Kernel的特征：

1.并发
并发：在一段时间内多个程序运行，需要OS管理和调度。
并行：在一个时间点上共同运行（因此只有一个CPU无法完成并行）。

2.共享
是“同时”访问还是互斥共享，根据情况而定。

3.虚拟
把硬件虚拟化。比如：把CPU虚拟化为进程，把磁盘虚拟化为文件，内存虚拟化为地址空间。
利用多道程序设计技术，让每个用户都觉得有一个计算机专门为他服务。

4.异步
程序执行不是一贯到底，而是走走停停，向前推进速度不可预知。
但只要运行环境相同，OS需要保证程序运行的结果也相同。
（异步双方不需要共同的时钟，也就是接收方不知道发送方什么时候发送，所以在发送的信息中就要有提示接收方开始接收的信息，如开始位，同时在结束时有停止位。）

操作系统的启动

通电之后，如何启动。

• DISK： 存放OS
• BIOS： 基本I/O处理系统。（检查各种外设）

在DISK上，还存在Bootloader，用于加载OS。

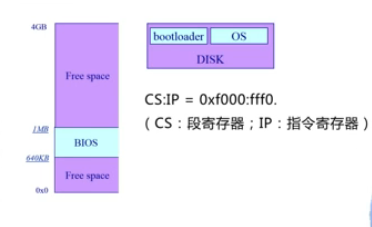
开始加电时，BIOS从CS:IP（图示为x86）这个地址开始执行，之后完成一系列工作，包括：

POST（加电自检）：寻找显卡和执行BIOS等。

BIOS加载Bootloader

Bootloader放在硬盘的第一个主引导扇区（512字节）。BIOS从硬盘的第一个扇区寻找，一下便找到Bootloader，Bootloader再负责加载OS。之后，由Bootloader将操作系统的代码和数据从硬盘加载到内存中。之后，控制权交给到OS。（跳转到OS的地址）

操作系统的interface（系统调用、异常、中断）

定义

• 系统调用（来源于应用程序的请求）

  应用程序主动向操作系统发出请求

• 异常（来源于不良的应用程序）

  非法指令或其他坏的处理状态（如：内存出错）

• 中断（来源于外设）

  来自不同的硬件设备的计时器和网络的中断

处理时间

• 异常： 同步 （知道什么时候产生，比如 除以0）
• 中断： 异步 （不知道什么时候产生）
• 系统调用： 异步或同步（返回过程可能是异步的，即系统处理完之后再告诉应用程序，应用程序再切回）

响应

• 异常： 杀死或重新执行 意想不到的应用程序指令。
• 中断： 持续，对用户应用程序是透明的（见不到）。
• 系统调用： 等待和持续。

终端和异常处理机制

中断、异常都有针对软硬件的处理过程。对中断和异常进行编号（中断表），编号对应特定地址，跳到处理历程，解决问题。
但是，中断打断了一个程序的正常执行，因此要设置保护与恢复机制。

• 中断
  硬件： ​ 1. 设置中断标记（CPU初始化），将内部、外部事件设置中断标记。​ 2. 产生中断号（中断事件ID），发给OS，OS来找到对应的处理历程。

​ 软件：

​ 1. 保存当前处理状态（保存被打断的执行现场。由OS完成）。

​ 2. 中断服务程序处理；

​ 3. 清除中断标记；

​ 4. 恢复之前保存的处理状态。因此，应用程序完全不用感知到中断的产生。

• 异常：异常编号

  1. 保存现场

  2. 异常处理

     2.1. 杀死产生了异常的程序

     2.2. 重新执行异常指令

  3. 恢复现场

• 系统调用

  1. 应用程序需要操作系统提供服务，而这些服务无法由应用程序直接执行，而需要操作系统执行，这就需要操作系统提供接口，这些接口就叫做系统调用接口。

  2. 程序访问主要是通过高层次的API接口而不是直接进行系统调用。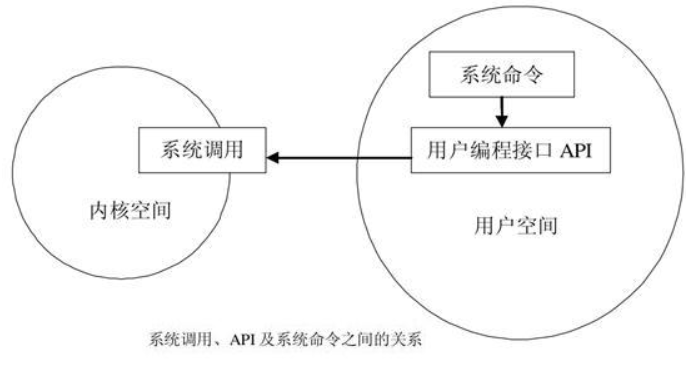

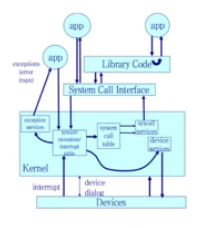
  3. 

一旦执行系统调用之后，用户态会转换为内核态

程序的用户态是指级别比较低的状态；
操作系统的内核态是等级最高的状态。可以控制整个计算机系统。

函数调用和系统调用是不同的。

函数调用：

ESP是栈指针寄存器，存储着栈顶的地址
EBP存储着栈底的地址
EIP是返回地址
栈空间主要通过这两个地址确定

结束func1，返回主程序过程类似。

函数调用是在一个栈空间完成函数之间参数的传递。

应用程序发出系统调用之后，应用程序、操作系统、内核都有自己的堆栈，要切换堆栈（操作系统堆栈与其不同，需要开销。即系统调用开销大于函数调用，但好处是安全、可靠），也要实现由用户态到内核态的转换。系统处理完之后，要把数据从内核空间拷贝到用户空间，接着实现状态转换。

（TLB（快表）：TLB是Translation Lookaside Buffer的简称，可翻译为“地址转换后援缓冲器。简而言之就是页表的Cache)

为什么应用程序不能直接访问外设呢？（必须要经过操作系统？）

在计算机运行中，内核是被信任的第三方。
只有内核可以执行特权指令。
为了方便应用程序。

计算机的体系结构及内存分层体系

计算机基本硬件结构

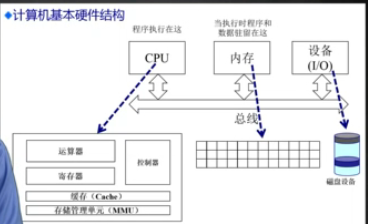
内存

内存的层次结构

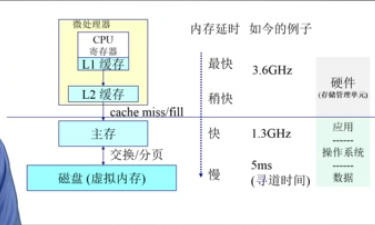
主存：物理内存

操作系统需要完成的一些事情

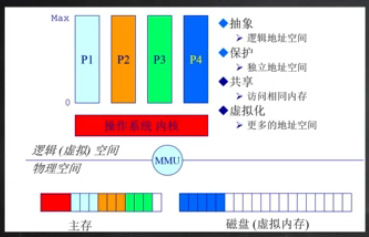
MMU: 内存管理单元（memory management unit)

• 抽象
• 保护
• 共享（进程间的数据传递机制）
• 虚拟化

在操作系统中管理内存的不同方法

• 程序重定位
• 分段
• 分页
• 虚拟内存
• 按需分页虚拟内存

地址空间和地址生成

几个问题：

               1. 什么是地址空间？逻辑地址空间和物理地址空间的区别？
               2. 地址空间是怎么生成的？什么时候生成逻辑地址空间？什么时候生成物理地址空间？
               1. OS如何保护不同的地址之间不受干扰？

地址空间

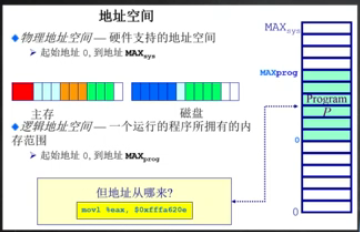
物理地址空间：主存、磁盘

逻辑地址空间：一个程序所看到的地址空间。所有的逻辑空间最终都落到物理空间内。

e.g.

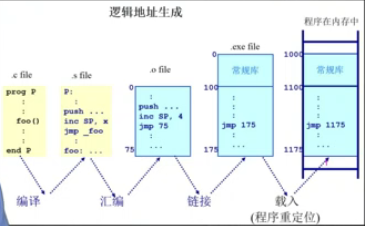
编译和汇编阶段，地址都是以变量名代表。

.c .s .o .exe程序都是放在硬盘之中， 最后的程序在内存中运行。可以看到运行时产生了内存偏移。

逻辑地址生成阶段，基本上不需要OS的参与。

即使程序放在内存中了，但其实还是逻辑地址，并不是物理地址。

CPU查找逻辑地址和物理地址的映射

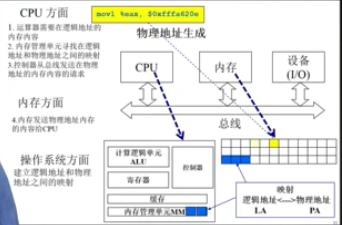
当CPU需要执行某条指令的时候：

 1. ALU需要知道指令的内容，需要发出请求，请求中所带的参数就是逻辑地址
 2. MMU会去查找逻辑地址映射表中是否存在逻辑地址对应的物理地址。
 3. 如果有，那么完成。如果没有，那么会产生处理过程，去内存中找（MMU没有）。如果找到了，CPU控制器会给主存发出请求，获取某一物理地址的内容。
 4. 主存会把内存的内容通过总线传给CPU，之后CPU开始执行。

在这个过程中，OS所做的操作就是需要在这些操作之前把映射关系建立好。

OS需要确保不同程序的地址不受干扰。加以限制和约束（如图）。

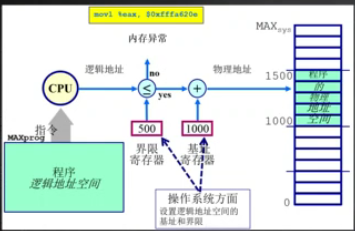
连续内存分配

内存碎片

• 无法进一步利用的空间。
• 外碎片： 分配单元间的碎片；
• 内碎片： 分配单元内没有使用的碎片

分区的动态分配

首次适配算法

碰到第一个能满足需求的空块，那么就分配。如图，需求400 byte，那么从低地址到高地址，可以看到第一块1K的就满足要求。

需求：

​ 按地址排序的空闲块列表。

​ 重分配需要检查，看自由分区能合并于相邻的空闲分区。

最优分配算法

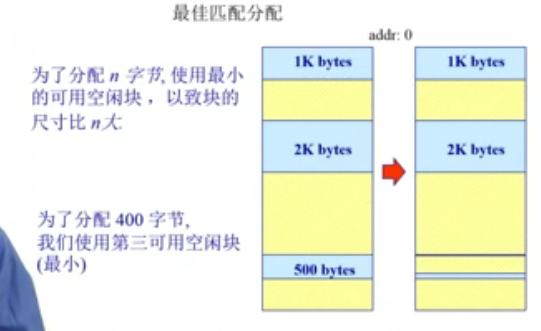
最差适配算法

压缩式碎片整理（紧致算法）

• 重置程序以合并孔洞
• 要求所有程序是 动态可重置的
• 问题？
  • 何时重置
  • 开销

交换式碎片整理

利用起硬盘，将等待中的程序所占用的内存放到硬盘上。

问题： 哪些程序进行交换？开销？（后续虚存管理会提及）

非连续内存分配

分段（更好的分离和共享）

• 程序的分段地址空间
• 分段寻址方案

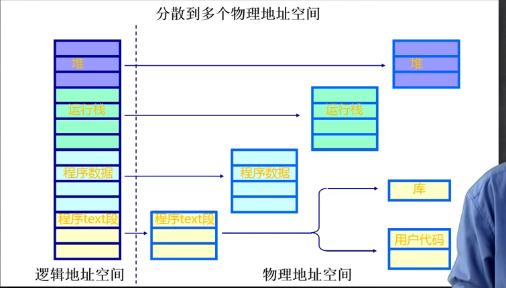
分段访问方案

• 段访问机制

操作系统在正式寻址之前建立段表

分页（目前cpu主要采取机制）

• 分页地址空间
• 页寻址方案

分页需要一个页号和一个页内偏移。

和分段机制的区别：段的尺寸是可变的，页的大小是固定不变的。

• 划分物理内存到固定大小的帧（frame）
  • 大小是2的幂
• 划分逻辑地址空间至相同大小的页（page）
  • 大小是2的幂
• 建立方案 转换逻辑地址为物理地址（pages to frames）
  • 页表
  • MMU/TLB（TLB叫快表）

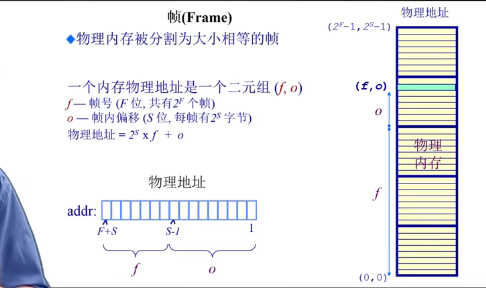
2^S 一帧的大小 f为帧号 o是页内偏移

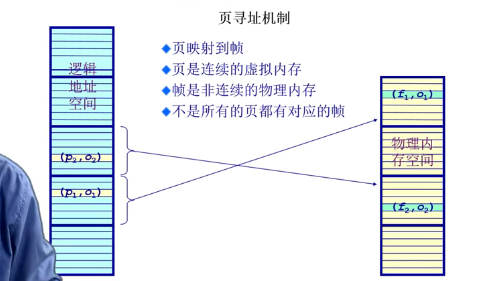
逻辑地址空间一般大于物理地址空间（存不下的会使用虚拟内存）

页表

• 页表概述
• 转换后备缓冲区
• 二级/多级 页表 （时间换空间）
• 反向页表

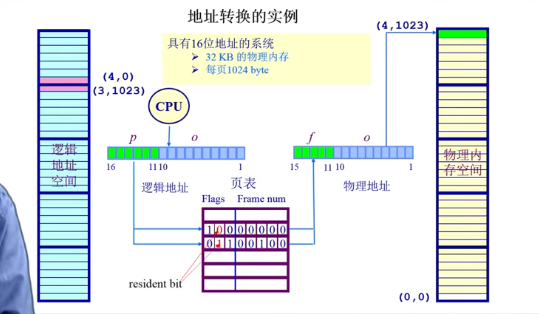
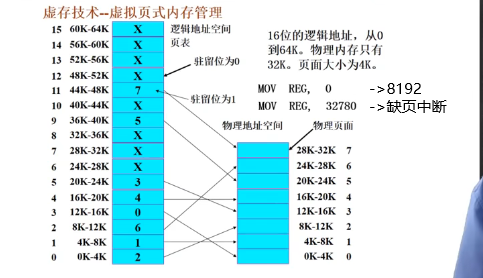
逻辑地址大小为64KB，物理地址大小为32KB

（4，0）-> 可以找到第四页100，页帧号均为0，说明不存在。产生内存访问异常。

（3，1023)->可以找到第三页011，页帧号为00100，页帧内偏移和页偏移相同为1023，可以得到（4，1023）

分页机制的性能问题

​ 1）访问一个内存单元需要两次内存访问：一次用于获取页表项，一次用于访问数据

​ 2）页表可能非常大。如64位及其如果每页1024字节，那么一个页表的大小为（2^64 /2^10 = 2^54），这是不合理的。 每个程序都有自己的页表，那么页表也非常大。

可以使用缓存（caching） ， 间接（indirecting）访问 两种方法来解决

TLB（Translation Look-aside Buffer）

把经常访问的页表项放到TLB中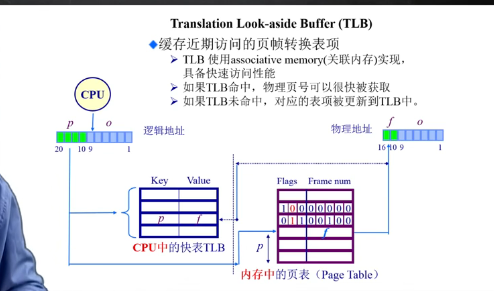

为了减少TLB的缺失，要注意程序的局部性。

二级页表

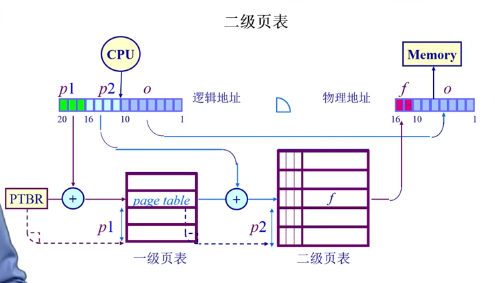
页表基寄存器（PTBR）指向页表. 页表长度寄存器（PTLR）指示页表的大小

一级页表存的是二级页表的起始地址

二级页表可以节省空间

e.g. 页面的大小为4KB，每个页表项为4B，所以每个页面中可以存放1K个（1024）个页表项，因此每1K个连续的页表项为一组，每组刚好占一个页面，这样就需要为离散的页表再建立一张页表，称为页目录表。

32位的逻辑地址空间，页表项大小为4B，页面大小4KB，则页内地址占12位将页表分为分为1024个表，每个表中包含1024个页表项，形成二级页表。二级页表结构的逻辑地址结构如下图：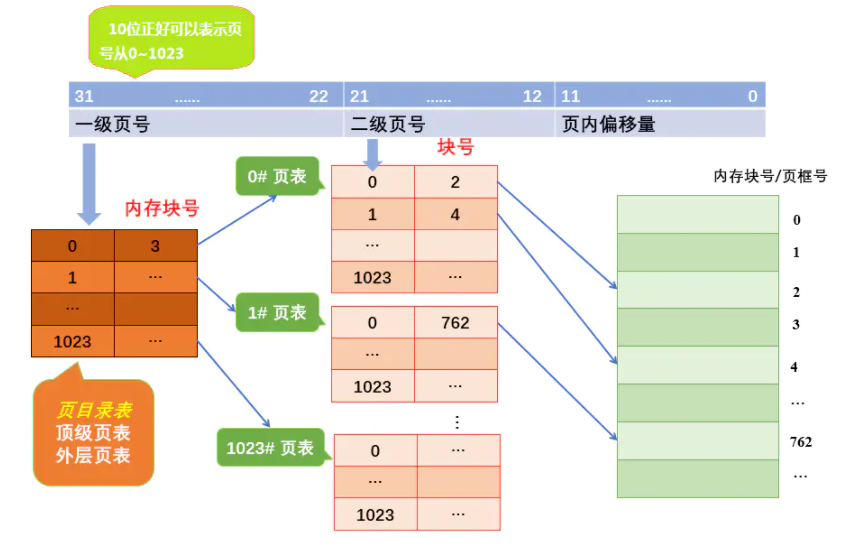

多级页表

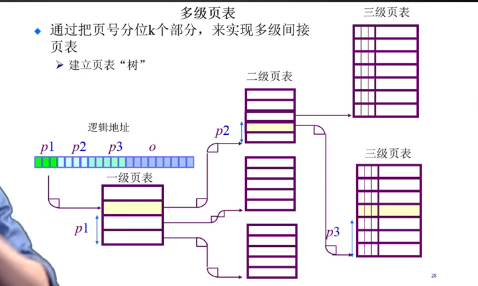
反向页表

以物理页号来查找逻辑页号

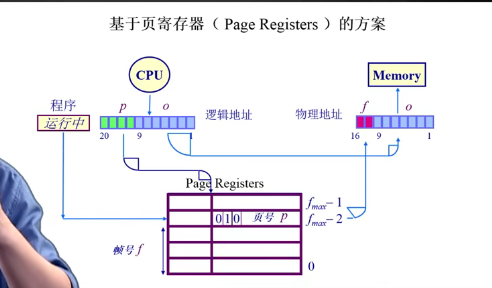
页容量只与物理页地址大小相关。好处是节省空间

问题：如何根据page frame号查找page号？

基于关联内存的方案（设计成本太大）

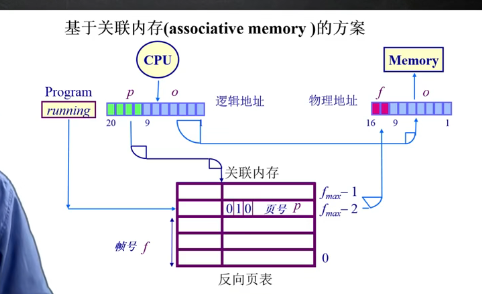
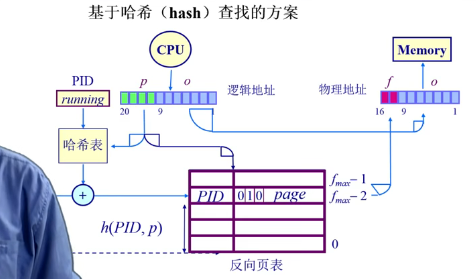
基于哈希（hash）查找的方案

page frame number （hash）-> page number

虚拟内存

• 起因 （程序规模的增长远大于存储器容量的增长）
• 覆盖技术
• 交换技术
• 虚存技术
  • 目标
  • 程序局部性原理
  • 基本概念
  • 基本特征
  • 虚拟页式内存管理

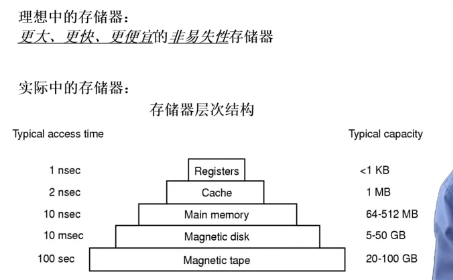
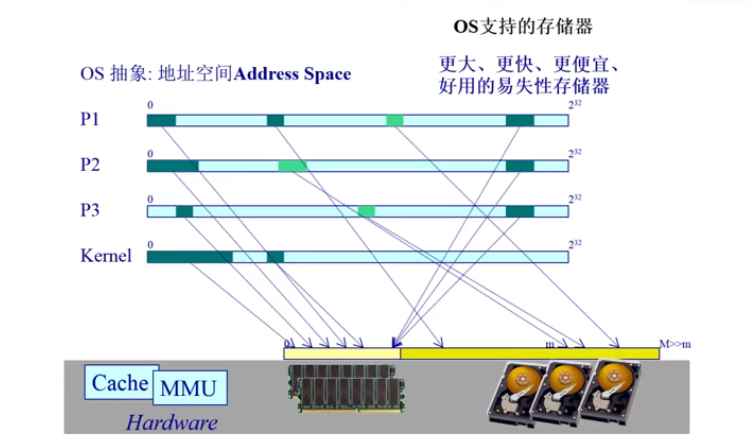
把一些希望通过OS的管理把不常用的数据放在硬盘，常用的数据放在内存中，这样使得有限的内存能够存放常用的代码和数据。这种管理方式需要CPU（硬件）、MMU（硬件）、OS内核协同管理之下可以实现。

覆盖技术

e.g.

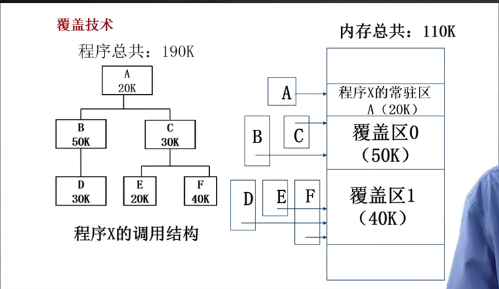
A在常驻区（固定区），把相互之间没有调用关系的程序放到同一个区，在需要调用前，再调入覆盖区，替换掉覆盖区原有的段。

注：另一种覆盖方法

​ A占一个分区20K

​ B、E和F 共用一个分区50K

​ C和D 共用一个分区30K

覆盖技术的缺点：

• 由程序员来把一个大的程序划分为若干个小地功能模块，并确定各个模块之间的覆盖关系，费时费力，增加了编程复杂度。
• 覆盖模块由外存装入内存，实际上是以时间来换取空间。

交换技术

交换技术的问题：

• 何时发生交换？ 因为内存和外存的读写速度差异太大，因此频繁的交换会造成巨大的开销，只当内存空间不够或有危险的时候换出。
• 如何划分硬盘，交换区的大小？
• 程序换入时的重定位。换出后和换入时的内存地址一定要是一样吗？可以采取动态地址映射来解决。

覆盖和交换的比较

交换发生在内存的程序之间，覆盖发生在运行中的程序之内。

虚存技术

虚存技术的目标：

• 像覆盖技术那样，不是把程序的所有内容都放在内存中，但是是自动执行的，无需程序员干涉；
• 像交换技术那样，实现进程在内存与外存之间的交换，但是不是以一个程序为粒度，而是以页为粒度。

e.g.

4byte x 1024 = 4k，正好是一页

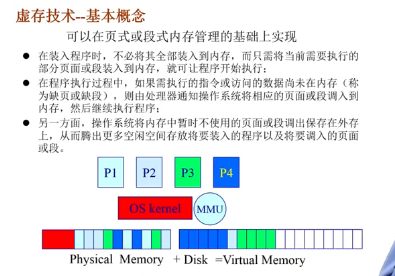
以页或段

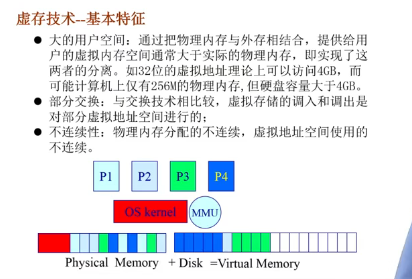
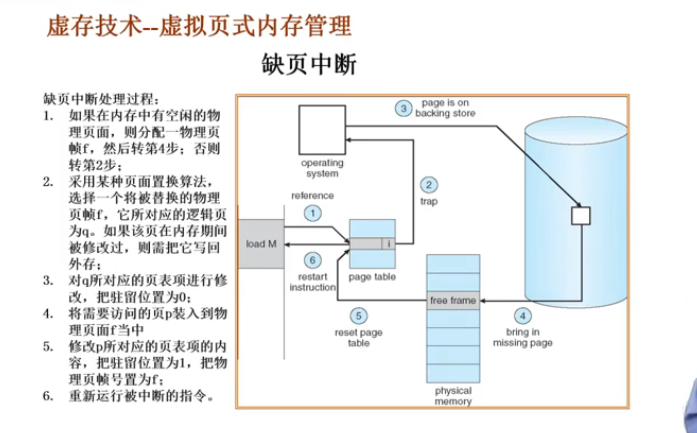
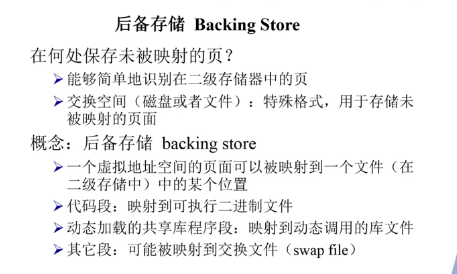
虚存技术--虚拟页式内存管理

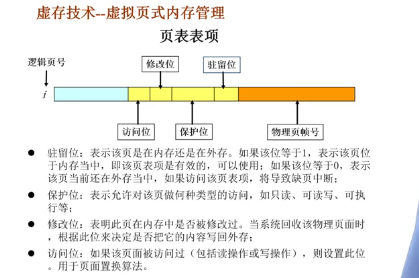
有效存储器访问时间（effective memory access time）

EAT = 访存时间 * 页表命中几率 + page fault处理时间 * page fault概率

页面置换算法（局部页面置换算法）

• 最佳页面置换算法（OPT）
• 先进先出算法
• 最近最久未使用算法
• 时钟页面置换算法

OPT以时间来记录，替换掉距离下一次访问最长时间内不被访问的页面

FIFO（队列），产生的缺页多

LRU是OPT的一个近似，LRU向之前看，OPT向后看

LRU算法需要记录每个页面使用时间的先后顺序，开销比较大。

二次机会法（改进型CLOCK置换算法），在使用位的基础上再增加一个修改位。

• 最近未被访问，也未被修改（u=0,m=0）
• 最近被访问，但未被修改（u=1,m=0）
• 最近未被访问，但被修改（u=0,m=1）
• 最近被访问，被修改（u=1,m=1）

计数器（寄存器的开销太大），每次寻找计数值最小的页面，开销也很大。

LFU存在的问题：一个页面在进程开始时使用的很多，但以后就不用了

页面置换算法（全局页面置换算法）

• 局部页替换算法的问题
• 工作集模型
• 工作集页置换算法
• 缺页率页面置换算法
• 抖动问题

局部页面置换算法问题

• 物理页帧大小对于置换算法性能影响极大。实际情况中，程序是分段进行的，物理页帧可变的，那该如何进行物理页帧大小分配？

工作集：一个进程当前正在使用的逻辑页面集合

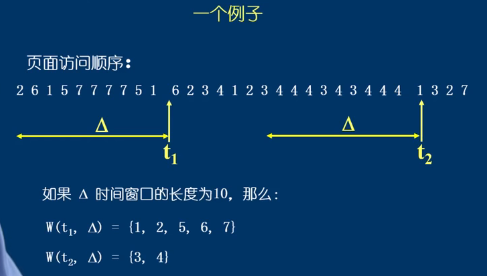
工作集页置换算法

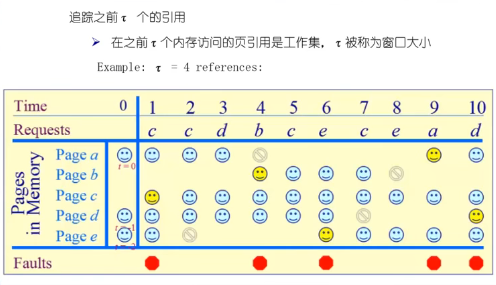
t=-2，访问page e

t=-1，访问page d

t=0，访问page a； 那么time0，初始化有三个页面

t=1，page c产生缺页，然后加入了page c， t=2时，未产生缺页，但是因为 τ = 4，所以要拿出page e。在拿出page e时候要判断该页是否修改过，若修改过那么需要进行内存和硬盘的同步。

缺页率页面置换算法

程序的编写，局部性影响缺页率。

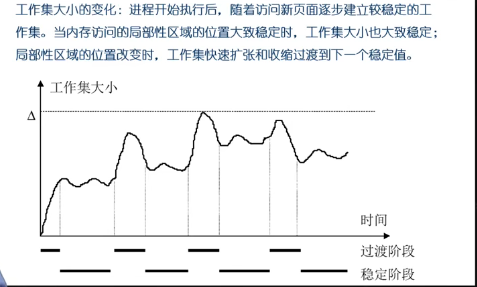
若运行的程序的缺页率过高。则通过增加工作集来分配更多的物理页面:若运行的程序的缺页率过低，则通过减少工作集来减少它的物理页面数。力图使运行的每个程序的缺页率保持在一个合理的范围内。

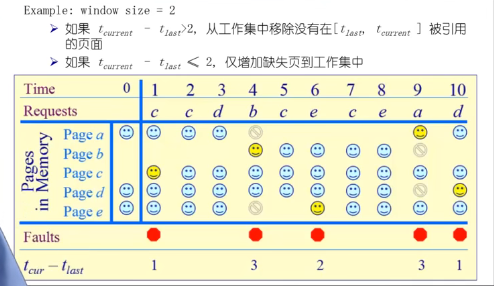
抖动问题

进程

进程的定义

一个具有一定独立功能的程序在一个数据集合上一次动态执行过程

进程的组成

进程的特点

• 动态性：可动态地创建、结束进程。
• 并发性：进程可以被独立调度并占用处理机运行。
• 独立性：不同进程的工作不相互影响。（页表等手段加以访问空间限制）
• 制约性：因访问共享数据/资源或进程间同步而产生制约。

进程控制结构

描述进程的数据结构：PCB（Process Control Block）。PCB是进程存在的唯一标志。

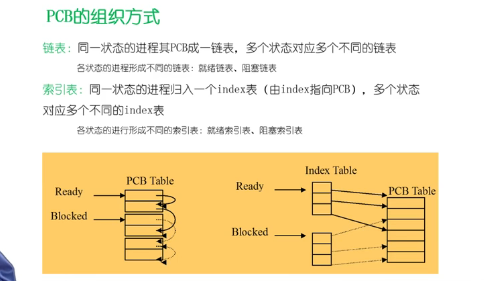
进程状态

• 进程的生命期管理
• 进程状态变化模型
• 进程挂起模型

进程的生命期管理

创建—运行—等待—唤醒—结束

进程创建

引起进程创建的3个主要事件：

1. 系统初始化时；
2. 用户请求创建一个新进程；
3. 正在运行的进程执行了创建进程的系统调用。

进程运行

内核选择一个就绪进程，让它占用处理机并执行。如何选择？此类问题将在调度算法中讨论。

进程等待

在以下情况下，进程等待（阻塞）：

1. 请求并等待系统服务，无法马上完成；
2. 启动某种操作，无法马上完成；
3. 需要的数据没有到达。

进程只能自己阻塞自己，因为只用进程自身才能知道何时需要等待某种事件的发生。

进程唤醒
进程唤醒的原因：

• 被阻塞进程需要的资源可以被满足。
• 被阻塞进程等待的事件到达。
• 将该进程的PCB插入到就绪队列。
• 进程只能被别的进程或者操作系统唤醒。

进程结束
在以下四种情况下，进程结束：

• 正常退出（自愿的）；
• 错误退出（自愿的）；
• 致命错误（强制性的）；
• 被其他进程所杀（强制性的）。

进程状态变化模型

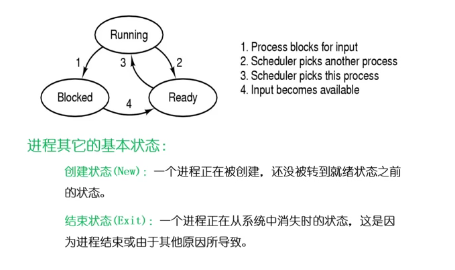
进程挂起模型

定义：进程没有占用内存空间。处在挂起状态的进程映像在磁盘上。

线程

定义：线程是进程当中的一条执行流程。

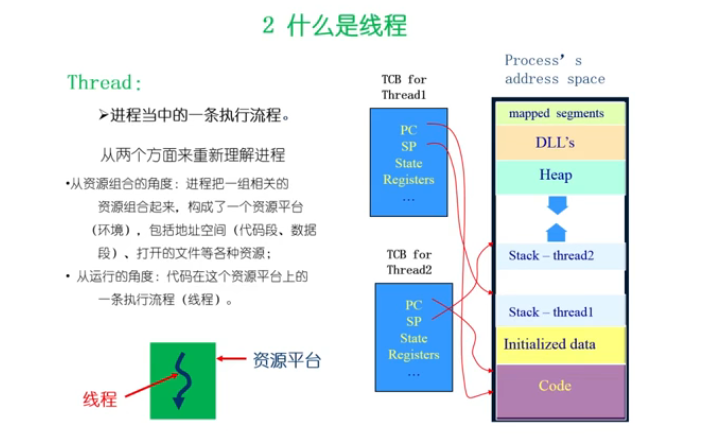
TCB（thread control block）

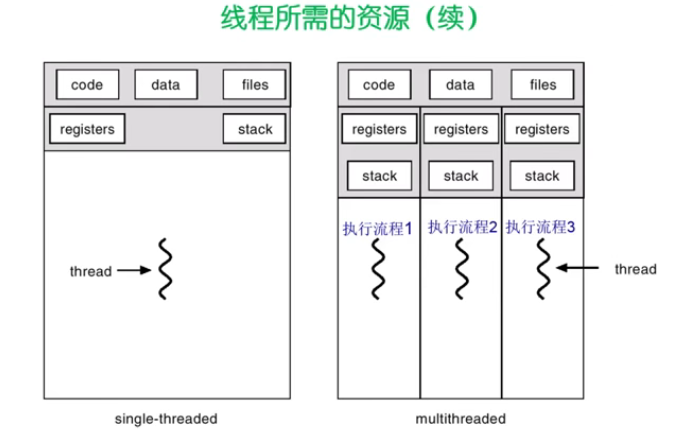
需要有各自独立的寄存器、堆栈，但是能共享代码段、数据段、网络资源等等，

线程的创建和终止时间较短是因为不需要去考虑资源的创建和释放问题。
线程的切换时间不需要切换内存管理所需要的页表，而进程需要切换页表，这一操作开销很大。

线程实现

用户线程和内核线程的关系

• 1对1
• 1对多
• 多对多

操作系统看不到TCB，OS只能看到进程信息，看不到进程内的线程信息。所以说整个线程的调度和管理主要是由线程库（用户级的线程库）管理，OS不直接参与。

用户线程：

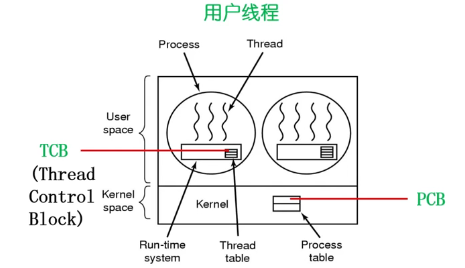
内核线程：

一个PCB管理了一个TCB的list，但是在具体的线程调度时，还是TCB进行

轻量级进程

定义：是内核支持的用户线程。一个进程可有一个或多个轻量级进程，每个量级进程由一个单独的内核线程来支持。

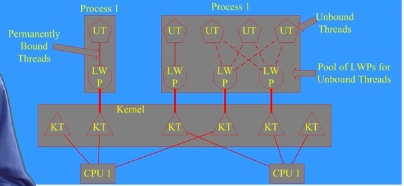
内核线程
内核线程只运行在内核态，不受用户态上下文的拖累。

• 处理器竞争：可以在全系统范围内竞争处理器资源；

• 使用资源：唯一使用的资源是内核栈和上下文切换时保持寄存器的空间

• 调度：调度的开销可能和进程自身差不多昂贵

• 同步效率：资源的同步和数据共享比整个进程的数据同步和共享要低一些。

轻量级进程
轻量级进程(LWP)是建立在内核之上并由内核支持的用户线程，它是内核线程的高度抽象，每一个轻量级进程都与一个特定的内核线程关联。内核线程只能由内核管理并像普通进程一样被调度。

轻量级进程由clone()系统调用创建，参数是CLONE_VM，即与父进程是共享进程地址空间和系统资源。

与普通进程区别：LWP只有一个最小的执行上下文和调度程序所需的统计信息。

• 处理器竞争：因与特定内核线程关联，因此可以在全系统范围内竞争处理器资源

• 使用资源：与父进程共享进程地址空间

• 调度：像普通进程一样调度

用户线程
用户线程是完全建立在用户空间的线程库，用户线程的创建、调度、同步和销毁全又库函数在用户空间完成，不需要内核的帮助。因此这种线程是极其低消耗和高效的。

• 处理器竞争：单纯的用户线程是建立在用户空间，其对内核是透明的，因此其所属进程单独参与处理器的竞争，而进程的所有线程参与竞争该进程的资源。

• 使用资源：与所属进程共享进程地址空间和系统资源。

• 调度：由在用户空间实现的线程库，在所属进程内进行调度

上下文切换

进程控制

创建进程

加载和执行进程

等待和终止进程

协程补充

进程： 进程是一个具有一定独立功能的程序关于某个数据集合上的一次运行活动，是系统资源分配和独立运行的最小单位；
线程： 线程是进程的一个执行单元，是任务调度和系统执行的最小单位；
协程： 协程是一种用户态的轻量级线程，协程的调度完全由用户控制。

进程与线程的区别

1、根本区别： 进程是操作系统资源分配和独立运行的最小单位；线程是任务调度和系统执行的最小单位。
2、地址空间区别： 每个进程都有独立的地址空间，一个进程崩溃不影响其它进程；一个进程中的多个线程共享该 进程的地址空间，一个线程的非法操作会使整个进程崩溃。
3、上下文切换开销区别： 每个进程有独立的代码和数据空间，进程之间上下文切换开销较大；线程组共享代码和数据空间，线程之间切换的开销较小。

当系统线程较少的时候没有什么问题，但是当线程数量非常多的时候，却产生了问题。一是系统线程会占用非常多的内存空间，二是过多的线程切换会占用大量的系统时间。

协程运行在线程之上，当一个协程执行完成后，可以选择主动让出，让另一个协程运行在当前线程之上。协程并没有增加线程数量，只是在线程的基础之上通过分时复用的方式运行多个协程，而且协程的切换在用户态完成，切换的代价比线程从用户态到内核态的代价小很多。

实际上协程并不是什么银弹，协程只有在等待IO的过程中才能重复利用线程，上面我们已经讲过了，线程在等待IO的过程中会陷入阻塞状态，意识到问题没有？

假设协程运行在线程之上，并且协程调用了一个阻塞IO操作，这时候会发生什么？实际上操作系统并不知道协程的存在，它只知道线程，因此在协程调用阻塞IO操作的时候，操作系统会让线程进入阻塞状态，当前的协程和其它绑定在该线程之上的协程都会陷入阻塞而得不到调度，这往往是不能接受的。

因此在协程中不能调用导致线程阻塞的操作。也就是说，协程只有和异步IO结合起来，才能发挥最大的威力。

那么如何处理在协程中调用阻塞IO的操作呢？一般有2种处理方式：

1. 在调用阻塞IO操作的时候，重新启动一个线程去执行这个操作，等执行完成后，协程再去读取结果。这其实和多线程没有太大区别。
2. 对系统的IO进行封装，改成异步调用的方式，这需要大量的工作，最好寄希望于编程语言原生支持。
   （https://zhuanlan.zhihu.com/p/172471249）

调度

• 上下文切换

  • 切换CPU的当前任务，从一个进程/线程到另一个。

  • 保存当前进程/线程在PCB/TCB中的执行上下文（CPU状态）。

  • 读取下一个进程/线程的上下文。

• CPU调度

  • 从就绪队列中挑选一个进程/线程作为CPU将要运行的下一个进程/线程。
  • 调度程序：挑选进程/线程的内核函数（通过一些调度策略）
  • 什么时候进行调度？

调度准则

• CPU使用率

​ CPU处于忙状态所占时间的百分比。

• 吞吐量

​ 在单位时间内完成的进程数量。

• 周转时间

​ 一个进程从初始化到结束， 所花费的时间。

• 等待时间

​ 进程在就绪队列中的时间。

• 响应时间

​ 从一个请求被提交到第一次产生响应 所花费的时间。

调度算法

• FCFS 先来先服务
• SPN(SJF) SRT 短进程优先（短作业优先） 短剩余时间
  • 可以是抢占的（SRT）或者是不可抢占的（SPN）
• HRRN 最高响应比优先
• Round Robin 轮循（时间片轮转调度算法）
• Multilevel Feedback Queues 多级反馈队列
  • 是时间片轮转调度算法和优先级调度算法的综合和发展，动态调整进程优先级和时间片大小。
• Fair Share Scheduling 公平共享调度

实时调度

实时调度所面对的系统为Real Time System（实时系统）。

对于实时系统：

• 时间约束的及时性（deadlines）很重要；
• 速度和平均性能相对不重要；
• 时间约束的可预测性是其主要特性。

实时系统可分为：

• 强实时系统：需要在保证的时间内完成重要的任务，必须完成；
• 弱实时系统：要求重要的进程的优先级更高，尽量完成，并非必须。

比如视频掉帧，就是弱实时系统的体现。

多处理器调度与优先反转

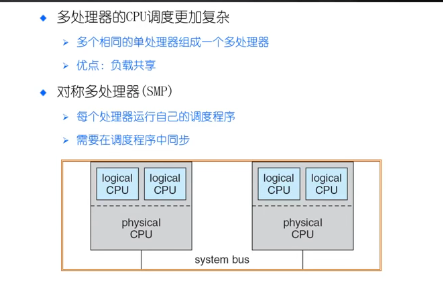
如何避免优先级反转：

优先级继承

优先级天花板

进程同步

进程之间的交互会造成共享资源的访问。

next_pid保存的是当前最大的进程ID。但是这种方法，在两个进程并行时，会产生冲突。

所谓原子操作是指不会被线程调度机制打断的操作；这种操作一旦开始，就一直运行到结束，中间不会有任何 context switch

临界资源

一次仅允许一个进程使用的资源称为临界资源。

临界区

临界区是指进程中的一段需要访问共享资源并且当另一个进程处于相应代码区域时便不会被执行的代码区域。

互斥

当一个进程处于临界区并访问共享资源时，没有其他进程会处于临界区并且访问任何相同的共享资源。

死锁

两个或以上的进程，在相互等待完成任务，而最终没法将自身任务进行下去。

饥饿（starvation）

一个可执行的进程，被调度器持续忽略，以至于虽然处于可执行状态却不被执行。

实现临界区互斥的基本方法

• 硬件实现方法

  禁用中断（中断屏蔽）

  当一个进程在使用处理机执行它的临界区代码时，防止其他进程进入临界区进行访问的最简单方法是，禁止一切中断发生。因为CPU只在发生中断时引起进程切换，但是在多CPU情况下，中断屏蔽不可使用，因为其他CPU还能访问临界区。

• 软件方法

​ 1. 单标志法

​ 2. 双标志法先检查

​ 3. 双标志发后检查

​ 4. Peterson’s Algorithm

​ P82

• 更高级的抽象

​

test-and-set是不允许执行中断的

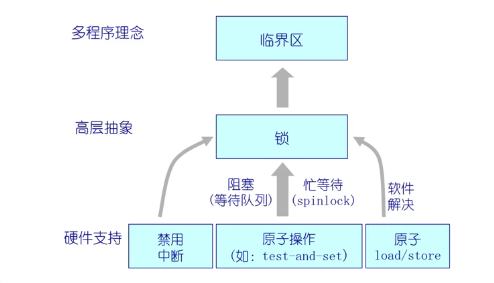
信号量

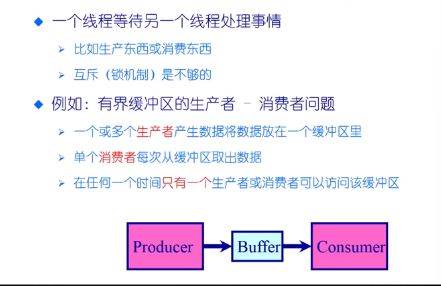
消费者问题需要引入同步和互斥操作。

P,V操作的顺序有影响，P操作能够产生阻塞。若Deposit交换前两个P操作，即先做mutex->P()，在执行emptyBuffers->p()，若生产者非常快，把fullbuffer填满了，那么下一个操作会执行mutex->P()，没问题，在下一个操作对emptyBuffer执行P操作，此时因为buffer满了，那么emptyBuffer为0，导致挂起，在此之后，消费者是没法执行操作的。陷入了死锁。

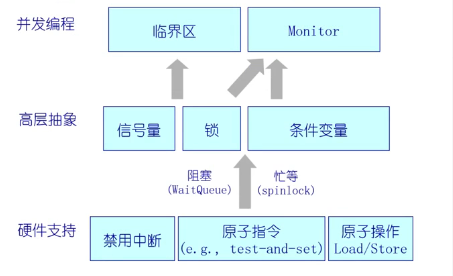
管程

比信号量的抽象程度更高。

目的：分离互斥和条件同步

定义：包含了一系列的共享变量（共享资源的数据结构），以及对该共享变量实时操作的一组过程。

要访问管程管理的那些函数只能有一个线程。

wait时一定要release，不然会导致无法释放lock，导致死锁。

用管程来解决生产者、消费者问题：

操作时一定要先上锁，优先满足进程互斥条件。

Hansen和Hoare方法

在管程中，A线程将B线程唤醒，是先执行A还是先执行B？Hanse和Hoare两位科学家给出了不同的解决办法。

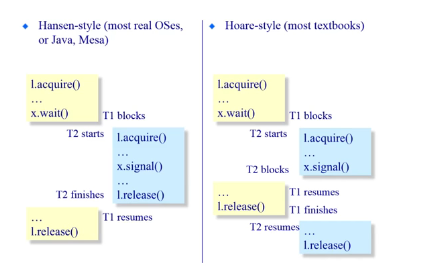
其中，Hansen机制较为容易实现（较为简单直观），实践中大量使用。

hansen使用while，release之后会造成多个等待进程抢占cpu资源。

hoare使用if，release之后只会有一个等待进程使用CPU。

经典同步问题

死锁

• 死锁问题
• 系统模型
• 死锁特征
• 死锁处理方法
  • 死锁预防
  • 死锁避免
  • 死锁检测
  • 死锁恢复

定义：是指多个进程因竞争资源而造成的一种僵局（互相等待）。

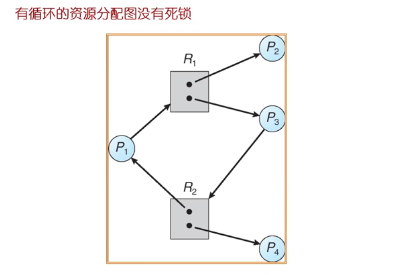
需要一个资源的情况下，没有死锁。

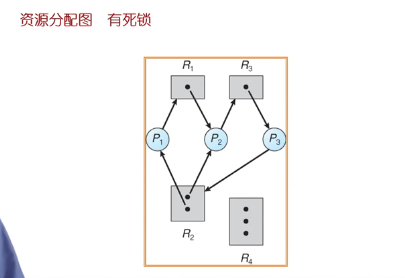
死锁一定产生环，有环不一定有死锁。

死锁产生的必要条件

有死锁产生，一定有这四种条件满足。满足这四种条件，不一定产生死锁。

1. 互斥条件

   在一个时间只能有一个进程使用资源。

2. 不剥夺条件

   以恶搞资源只能被进程自愿释放。

3. 请求并保持条件

   进程保持至少一个资源正在等待获取其他进程持有的额外资源。

4. 循环等待条件

   存在等待进程集合 [P0, P1, … , PN] ，产生环。

死锁的处理策略

1. 死锁预防

   设置某些限制条件，破坏产生死锁的4个必要条件中的一个或几个，以防止死锁产生。

2. 死锁避免

   在资源的动态分配过程中，用某种方法防止系统进入不安全状态，从而避免死锁。

3. 死锁检测

   无需采取任何限制性措施，允许进程在运行过程中发生死锁。通过系统的检测机构及时地检测出死锁的发生，然后采取某种措施解除死锁。

死锁预防

破坏死锁产生的4个必要条件之一。

死锁避免

避免死锁同样属于事先预防策略，并不是在事先采取某种限制措施破坏死锁的必要条件，而是在资源动态分配过程中，防止系统进入不安全状态，以避免发生死锁。

系统安全状态

是指系统能够按某种进程推进顺序为每个进程分配其所需的资源，直至满足每个进程对资源的最大需求，使每个进程都可顺序完成。

银行家算法

把操作系统视为银行家，操作系统管理的资源相当于银行家的资源，进程向操作系统请求分配资源相当于用户向银行家贷款。

进程运行之前先声明对各种资源的最大需求量，当进程在执行中继续申请资源时，先测试该进程已占用的资源数与本次申请的资源数之和是否超过该进程声明的最大需求量。若超过则拒绝分配资源，若未超过则再测试系统现存的资源能否满足该进程尚需的最大资源量，若能满足则按当前的申请量分配资源，否则也要推迟分配。

并非所有的不安全状态都是死锁状态，但当系统进入不安全状态之后，便可能进入死锁状态。反之，只要系统处于安全状态，系统便可避免进入死锁状态。

银行家算法

安全性算法

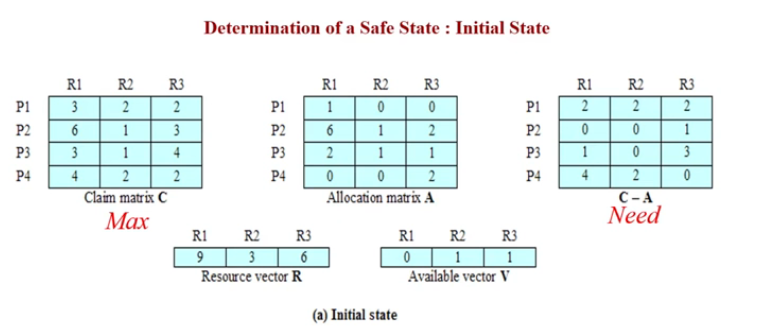
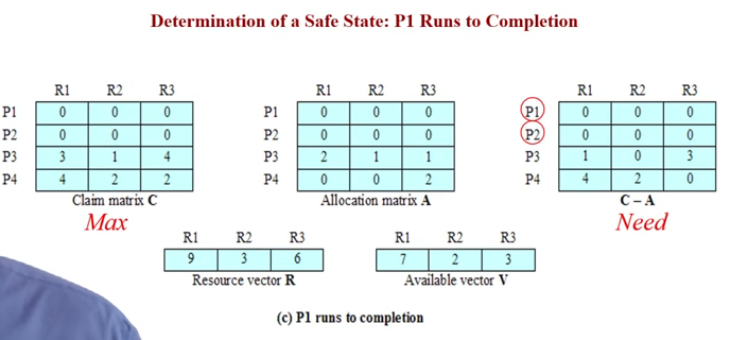
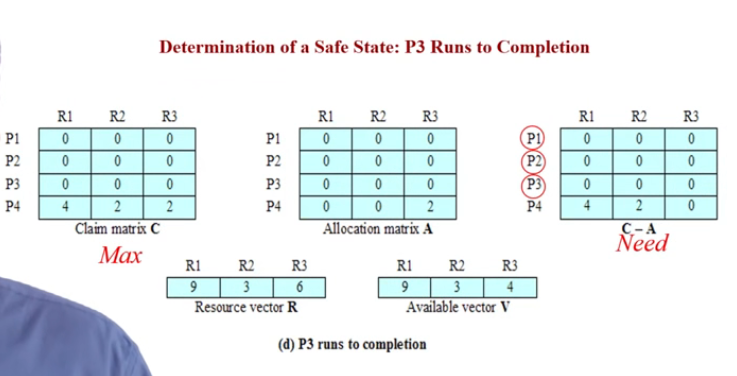
同理P4。

P2-P1-P3-P4是个安全状态

死锁检测和死锁恢复

死锁检测

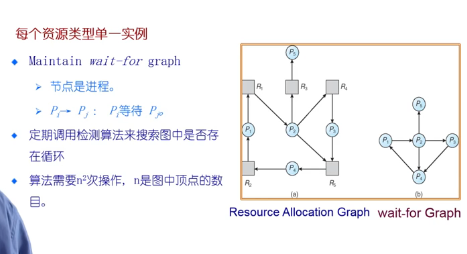
把资源分配图做一定的简化，变为一个等待图（去掉资源节点，只留下进程节点）

死锁恢复（死锁解除）

1. 资源剥夺

   挂起某些死锁进程，并剥夺它的资源，

2. 撤销进程

   强制撤销部分甚至全部死锁进程并剥夺这些进程的资源。

3. 进程回退

   让一个或多个进程回退到足以回避思死锁的地步，进程回退时自愿释放资源而非被剥夺。

进程间通信（IPC InterProcess Communication）

消息传递

1. 直接通信方式
2. 间接通信方式

进程间通信常用的手段

信号

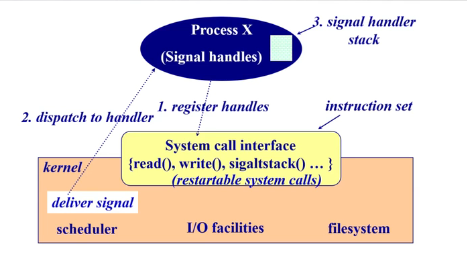
管道

管道是用来数据交换的。

管道通信中，存储空间进化成了缓冲区，缓冲区只允许一边写入、另一边读出，因此只要缓冲区有数据，进程就能从缓冲区中读出，而不必担心会因为其他进程在其中进行写操作而遭到阻塞，因为写进程会先把缓冲区写满，才让读进程读，当缓冲区中还有数据时，写进程不会向其中写数据。

管道通信必然是双半工通信。

消息队列

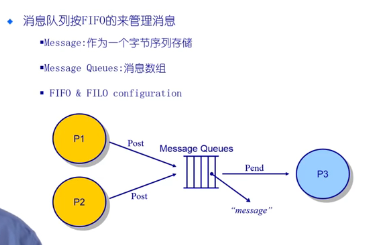
有buffer的size限制，当满或空，也会出现sleep机制。

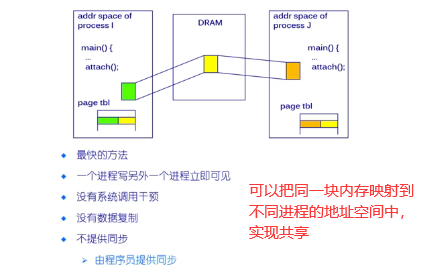
共享内存

1. ostream 的重载。

2. 宏定义函数。

   1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19

   const char* LogLevel::ToString(LogLevel::Level level){ switch(level){ #define XX(name) \ case LogLevel::name: \ return #name; \ break; // “\” 是换行继续的意思 // #name 表示使用传入的“参数名称”字符串，注意不是name值本身 XX(DEBUG); XX(INFO); XX(WARN); XX(ERROR); XX(FATAL); # undef XX default : return "UNKNOWN"; } return "UNKNOWN"; }

3. 流对象是不能复制的。

   1	virtual void format(std::shared_ptr<Logger> logger, std::ostream& os, LogLevel::Level level, LogEvent::ptr event) = 0;

   第一次写的为std::ostream os
   我在log.cc中使用时，a->format(logger, ss, level, event);
   报错为：Calling a protected constructor of class ‘std::basic_ostream
   后续修改为 std::ostream& os 才通过

4. auto self = shared_from_this(); //返回一个当前类的std::shared_ptr
   shared_from_this 是个模板类，要让使用shared_from_this()的类继承才可使用
   如 log.h之中的 class Logger : public std::enable_shared_from_this
   我们可通过这种方法来使用智能指针去控制对象的生存周期

5. 函数表与函数容器

   <<C++ Primer>>第五版第十四章

   函数表（function table）是表示函数映射关系的表，常使用map<>来映射 std::string 和 std::function<>。

   函数容器的类型是

6. 我们可以为一个或多个实参定义默认值（默认实参 default argument），不过一旦某个形参被赋予了默认值，它后面所有的形参都必须有默认值。

7.  int main(int argc, int** argv){   //  or  int main(int argc, int* argv[]){}
    
    }
   

   argc是命令行的总参数个数。
   argv[]有argc个参数，其中第0个参数是程序全名，命令行后面跟的用户输入的参数。
   char *argv[]是一个字符数组，其大小是argc，主要用于命令参数argv[]参数。
   数组里每一个元素代表一个参数。

   eg： 输入 test， a.c ，b.c， t.c 则 argc=4；
   argv[0]=test;
   argv[1]=a.c;
   argv[2]=b.c;
   argc[3]=t.c;

8. 几种特殊标准定义

   __FILE__ : 正在编译文件的文件名

   __LINE__ : 正在编译文件的行号

   __DATE__ : 编译时刻的日期字符串

   __TIME__ : 编译时刻的时间字符串

   __STDC__ : 判断该文件是不是标准C程序

环境配置

virtualbox

centos 7.9

ohmyzsh

vim

GCC

GDB

CMAKE

ragel

boost

其他

Linux 修改 /etc/sysconfig/network-scripts/ifcfg-enp0s3 => ONBOOT=YES

修改 VirtualBox 网络模式为 桥接网卡 ( ip addr看网卡几为broadcast)

ping ip addr inet地址测试

执行 service network restart

若ping通但是ssh连接不上

1） 首先要确保centos安装过了 openssh-server , 终端输入 yum list installed | grep openssh-server

这表示已经安装了，若没有内容则表示没安装

使用 yum install openssh-server 安装

2）找到 /etc/ssh/ 目录下的sshd的配置文件 ssha_config, 将文件中的 Port, ListenAddress前的注释符号**#**去掉， 然后打开远程登录 PermitRootLogin yes, 选择验证为 PasswordAuthentication yes.

3）开启sshd服务，输入sudo service sshd start

接着检查sshd是否已经打开 , ps -e | grep sshd

也可以 netstat -an | grep 22检查 22 端口是否开启监听（状态为LISTEN）

4）虚拟机和主机互相ping

若主机ping不通虚拟机，那么为虚拟机防火墙的问题

若虚拟机不能ping通主机，那么打开windows防火墙的ICMPv4-in规则

termius 连接，默认端口就行（我写了个端口反而不行

安装 ohmyzsh

这是一个命令解释器

官网复制命令安装

换到码云安装，githubusercontent 老报错

sh -c “$(curl --insecure -fsSL https://gitee.com/shmhlsy/oh-my-zsh-install.sh/raw/master/install.sh)"

安装VIM

注意与C++的版本兼容

安装依赖

yum install wget
yum install ncurses-devel
yum install gcc gcc-c++
yum install ctags
yum install bzip2

wget ftp://ftp.vim.org/pub/vim/unix/vim-8.1.tar.bz2
tar xvf vim-8.1.tar.bz2 (解压)
cd vim81
./configure --prefix=/apps/webserver （编译时指定路径）
make -j4 （make -j带一个参数，可以把项目在进行运行编译，让make最多允许4个编译命令同时执行）
make install

#验证安装成功
which vim
/apps/webserver/bin/vim (我使用configure指定位置安装老是装不上，后来默认了)

git clone https://github.com/sylar-yin/myvim.git
cp myvim/.vim / -rf
cp myvim/.vimrc ~/ （路径代表用户根目录，/路径代表最顶层根目录）

alias vctags=”ctags -R --c++-kinds=+p --fields=+iaS --extra=+q”
添加到/etc/profile末尾

GCC安装

wget “http://ftp.gnu.org/gnu/gcc/gcc-9.2.0/gcc-9.2.0.tar.gz"
这个包下载比较快

安装bison

yum install bison

安装texinfo

yum install texinfo

添加自定义安装路径到PATH

export PATH=/apps/webserver/bin:$PATH
export LD_LIBRARY_PATH=/apps/webserver/lib:/apps/webserver/lib64:$LD_LIBRARY_PATH
将这条语句添加到~/.profile 或者 /etc/profile 文件最后。

安装autoconf

gcc安装需要依赖automake-1.15以上版本，automake-1.15以上版本，需要依赖autoconf 2.69

wget http://ftp.gnu.org/gnu/autoconf/autoconf-2.69.tar.gz
tar xvf autoconf-2.69.tar.gz
cd autoconf-2.69
./configure --prefix=/apps/webserver
make -j4
make install

#验证安装成功
which autoconf
/apps/webserver/bin/autoconf

安装automake

gcc安装需要依赖automake-1.15以上版本

wget http://ftp.gnu.org/gnu/automake/automake-1.15.tar.gz
tar xvf automake-1.15.tar.gz
cd automake-1.15
./configure --prefix=/apps/webserver
make -j4
make install

#验证安装成功
which automake
/apps/webserver/bin/automake

开始安装GCC

wget “http://ftp.gnu.org/gnu/gcc/gcc-9.2.0/gcc-9.2.0.tar.gz"
（安装时间巨长，等就行了）
tar xvf gcc-9.1.0.tar.xz
cd gcc-9.1.0
sh contrib/download_prerequisites
mkdir build
cd build
../configure --enable-checking=release --enable-languages=c,c++ --disable-multilib --prefix=/apps/webserver
make -j4
make install

#验证安装成功
which gcc
/apps/webserver/bin/gcc

查看gcc版本是否一致，若不是安装版本，则进入到gcc x.x/build文件夹，输入source /etc/profile

安装GDB

linux下使用GDB调试
gdb需要在gcc安装完成之后再安装

wget http://ftp.gnu.org/gnu/gdb/gdb-8.3.tar.xz
tar xvf gdb-8.3.tar.xz
cd gdb-8.3
./configure --prefix=/apps/webserver
make -j4
make install

#验证安装成功
which gdb
/apps/webserver/bin/gdb

安装cmake

wget https://github.com/Kitware/CMake/releases/download/v3.14.5/cmake-3.14.5.tar.gz

其余版本 https://cmake.org/download/

tar xvf cmake-3.14.5.tar.gz
cd cmake-3.14.5
./configure --prefix=/apps/webserver
make -j4
make install

#验证安装成功
which cmake
/apps/webserver/bin/cmake

安装Ragel

wget http://www.colm.net/files/ragel/ragel-6.10.tar.gz
tar xvf ragel-6.10.tar.gz
cd ragel-6.10
./configure --prefix=/apps/webserver
make -j4
make install

#验证安装成功
which ragel
/apps/webserver/bin/ragel

安装其他软件

yum install boost-devel
yum install psmisc (killall安装)
yum install net-tools (netstat安装)

EBO概念

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31

#include <iostream>

using namespace std;

class A {};

class B1 {
private:
	A a;
};

class B2 {
private:
	A a;
	int x;
};

class C:private A {
private:
	int x;
};


int main() {

	cout << sizeof(A) << endl;
	cout << sizeof(B1) << endl;
	cout << sizeof(B2) << endl;
	cout << sizeof(C) << endl;
	return 0;
}

输出结果为

对于A这样一个空类，编译器会给这个空类安插一个char，来标识这个类。

对于B，由于字节对齐，B将占用8个字节。

对于B1来说，A的大小为1，int大小为4，一共为5，字节补齐将其补齐为8(4的倍数)。

对于B2来说，直接继承然后添加一个int，空间为5，并未进行补齐。1的补齐所浪费的空间是巨大的。EBO机制存在的意义就在此。

1
2
3
4
5
6
7
8
9
10
11
12
13
14

class Empty {};

class Empty1 : public Empty {};

class Empty2 : public Empty1 {};

class Empty3 : public Empty,Empty1 {};


//sizeof(Empty) == 1     <- EBO机制
//sizeof(Empty1) == 1    <- EBO机制
//sizeof(Empty2) == 1    <- EBO机制
//sizeof(Empty3) == 1    

前三个都是EBO的体现，但是Empty3继承了两次Empty，不符合EBO的规则，但实际上Empty3的大小仍为1。

:(===为啥是1===

EBO的准则：只有空类对象不与同一类型的其他对象或子对象分配在同一地址，就不需要为其分配空间。

同一地址的问题，即使是同一类型的对象只有分配地址不同，也不需要为其分配空间

我理解的不好，网址插个旗

https://blog.csdn.net/zhangxiao93/article/details/76038001