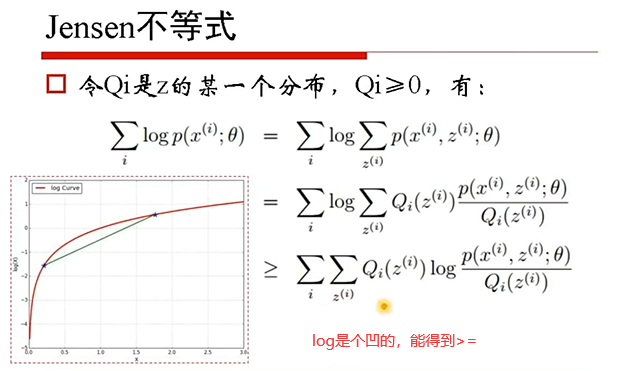
运筹优化知识

发表于 更新于

链表

optimization problem

  1. 无约束的优化问题
  2. 带等式约束的优化问题
  3. 带不等式约束的优化问题

dual

KKT

经典注水问题：
$$
min -\sum^n_{i=1}log(\alpha + x_i) \
s.t.~~~~~~~~ x \geq, 1^Tx=1
$$
其中$\alpha_i >0$ 。

令$x^*$ and $(\lambda^*,v*)$分别是原问题和对偶问题的某对最优解，对偶间隙为0，可以得到如下的KTT条件：
$$
x^* > 0,~~~ 1^Tx^*=1,~~~\lambda^\succeq0,~~~ \lambda_i^x_i^*=0,i=1…n, \
\frac{-1}{\alpha_i + x_i^*}-\lambda_i^*+v^*=0, i=1…,n
$$
$\lambda^*$在最后一个方程里是一个松弛变量，可以消去。
$$
x^* > 0,~~~ 1^Tx^*=1,~~~\lambda^\succeq0,~~~ x_i^(v^* - \frac{1}{\alpha_i + x_i^*})=0,i=1…n, \
v^* \geq \frac{1}{\alpha_i + x_i^*}, i=1…,n
$$
所以有下式：
$$
x_i^*=\left{ \begin{aligned} &\frac{1}{v^*}-\alpha_i, &v^* < \frac{1}{\alpha^*} \
&0 , &v^\geq \frac{1}{\alpha^}
\end{aligned}
\right.
$$
更简洁地，$x^* = max{\frac{1}{v^*} - \alpha_i, 0}$, 将该值代入条件$1^Tx^*=1$，可以得到
$$
\sum^n_{i=1}max{ 0,\frac{1}{v^*}-\alpha_i }=1
$$

单纯形法

单纯形算法适用的情况

标准的线性规划格式
$$
& max~~~ c^Tx \
& ~~~~~~~~~s.t. ~~~A*x \leq b \
&~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~ x_i \geq 0, i = 1,2,3,…,n
$$
松弛型

image-20220411162221373

主问题是 $2x_1 + x_2$, 不是$x_3$

加入非负松弛变量

image-20220411162306991

单纯形

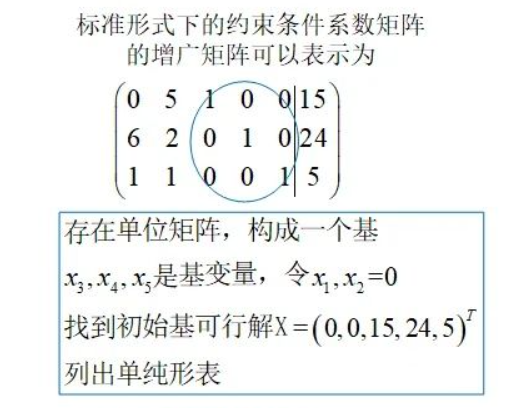
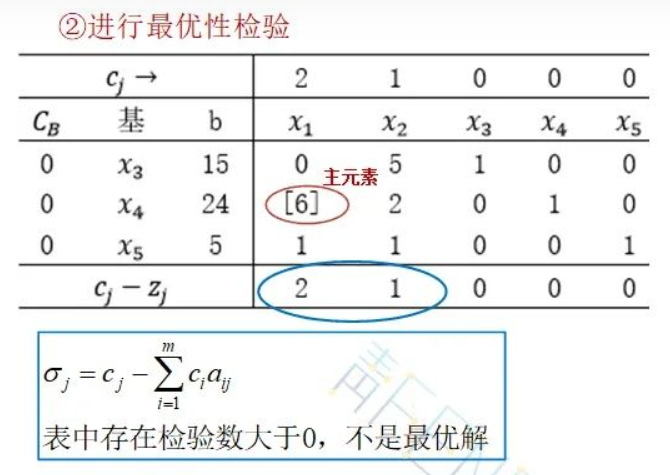
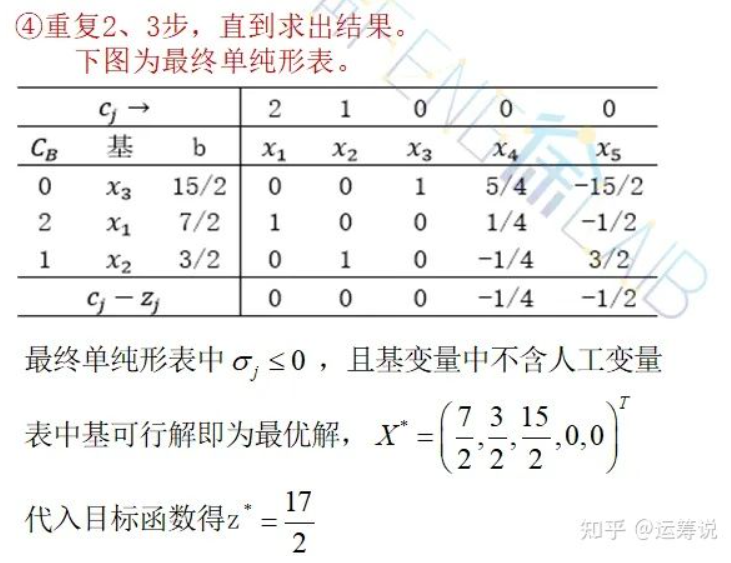
image-20220411162333695 image-20220411162348367 image-20220411162407384 image-20220411162420712

ref: https://zhuanlan.zhihu.com/p/388224103

影子价格

Row Generation（就是割平面法）

常用于整数规划

割平面方法，从更宏观的角度，可以看作是一种行生成方法。这里的“行”（row），指的是线性不等式。每找到一个cut，就增加一个线性不等式。

线性规划的算法复杂度和连续变量呈多项式级关系，另外随着约束条件（不等式）个数的增加，求解时间也会随之增加。（不确定呈什么关系，求拍砖）

上面说到整数规划的算法复杂度和整数变量的个数n基本呈指数关系，那么它还和其他什么因素相关呢？答案是不等式的个数。（recall求解整数规划需要求解一个个的线性规划）

我们从线性规划角度，理解行生成方法的基本思想：形成极值（最优解）所需要的约束条件个数，往往远小于原问题的约束条件个数。因此为何不在需要的时候，才把这些“重要”的约束条件加上来呢？

下面举个简单例子：

如下图，原问题有5个不等式（一条红线代表一个不等式），但是最优解点D只需CD和DE 2个不等式即可表述。

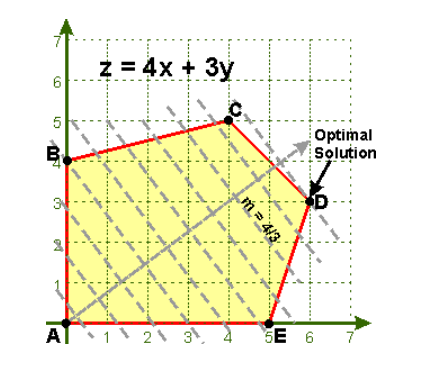
image-20220412174455417

因此行生成方法的基本思路：先求解原问题的松弛问题，即初始问题（master problem）不加约束条件或只加其中几个约束，然后求解该松弛问题，如果得到的解是可行解，那么该解就是原问题的最优解（例如刚开始运气很好地加了CD和DE）。

如果得到的解对原问题是不可行的，例如解是（0，6）这个点（因为没有加BC这个约束），或者无界的，那么这时候加上BC这个不等式便可以把这个不可行解排除。

以此循环，直到松弛问题的解是可行的，那么该解也是原问题的最优解。

而通过行生成方法，上面问题本来需要5个约束条件，很可能只需要2-3个约束条件，上面的循环已经终止了。

在实际问题中，最优解所需要的约束条件往往远远小于原问题的约束条件个数。例如几万个约束条件，实际只有几百个是用来刻画最优解的。那么这个时候，割平面方法便可以大大提速线性规划的求解。

在上一节的TSP问题中，subtour elimination constraints的个数是指数级的（因此不可能把他们全部加进来），但是求解实际问题中，往往通过割平面方法只需找到其中几千或几百个，即可找到原问题的最优解。用到的，正是相似的思路。

其实TSP问题是有完整刻画的表达式的（Complete Formulation），这时的约束个数虽然不是指数级，但是数量也非常大，因此求解效率很低。割平面方法的引入，大大增加了TSP问题求解的高效性，这也是该方法一次完美的show off。

搜索Literature 行生成方法，最先映入眼帘的可能是Benders’ Decomposition。在那里，一般把整数和实数变量隔离做分解，然后有比较“严格”的如何选取初始约束以及如何一步步地增加约束（feasibility cut和optimality cut）。

与行生成法对偶的方法，是列生成法（逐步增加变量个数）。其中的Dantzig-Wolfe分解法，是Benders’ Decomposition的dual problem。

ref: https://zhuanlan.zhihu.com/p/28387290?group_id=893712252413284352

column generation

列生成算法（Column Generation Algorithm）是一种用于求解大规模线性优化问题的高效算法，本质上来讲，列生成算法是单纯形法的一种形式，用来求解线性规划问题。

列生成算法已被应用于求解很多著名的NP-hard优化问题，如机组人员调度问题（Crew assignment problem）、切割问题（Cutting stock problem）、车辆路径问题（Vehicle routing problem）、单资源工厂选址问题（The single facility location problem）等

基本思想

列生成算法通过求解子问题（sub problem）来找到可以进基的非基变量，该非基变量在模型中并没有显性的写出来（可以看成是生成了一个变量，每个变量其实等价于一列，所以该方法被称为列生成算法）。如果找不到一个可以进基的非基变量，那么就意味着所有的非基变量的检验数（Reduced Cost，RC）都满足最优解的条件，也就是说，该线性规划的最优解已被找到。其思路如下：

1、先把原问题（Master Problem，MP）转换到一个规模更小（即变量数比原问题少）的问题上，这个只使用部分变量的模型被称为原问题的RMP 问题（Restricted Master Problem）。在RMP上用单纯形法求最优解，注意此时求得的最优解只是RMP上的，并不是MP的最优解。

2、然后需要通过一个子问题去检测在那些未被考虑的变量中是否有使得RC小于零的情况，如果有，那么就把这个变量的相关系数列加入到RMP的系数矩阵中，返回第1步。

经过反复迭代，直到子问题中的RC都大于等于零，此时就找到了MP的最优解。

注意min和max问题的影子价格

拉格朗日松弛

拉格朗日对偶（问题）

bender’s decomposition

主要思想是行生成+割平面方法

single bender’s

multi bender’s

branch and bound（精确算法）

分支定界

分支定界算法始终围绕着一颗搜索树进行的，我们将原问题看作搜索树的根节点，从这里出发，分支的含义就是将大的问题分割成小的问题。大问题可以看成是搜索树的父节点，那么从大问题分割出来的小问题就是父节点的子节点了。分支的过程就是不断给树增加子节点的过程。而定界就是在分支的过程中检查子问题的上下界，如果子问题不能产生一比当前最优解还要优的解，那么砍掉这一支。直到所有子问题都不能产生一个更优的解时，算法结束。

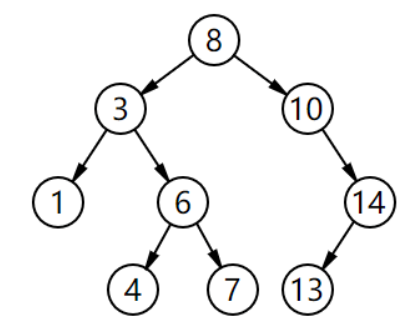
image-20220412155612418

例子

对于一个整数规划模型：
$$
maximize~~~~~~&4x_1+9x_2+6x_3 \
subject~ to~~~~&5x_1+8x_2+6x_3 \leq 12 \
&x_1,x_2,x_3 ~ are~ binary~ variable
$$
因为求解的是最大化问题，不妨先设当前的最优解为负无穷：-INF。

  1. 首先从主问题分出两支子问题：
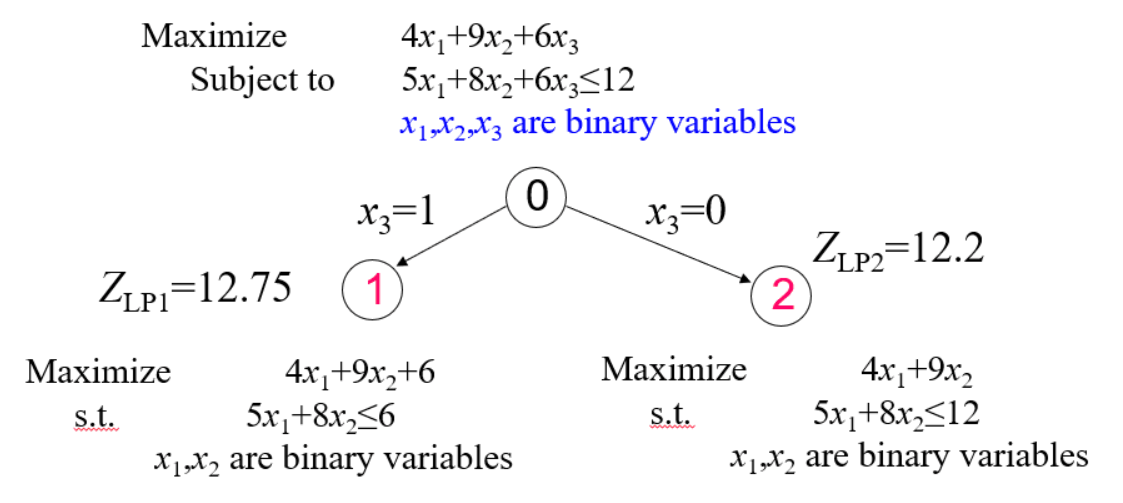
image-20220412160043235

通过线性松弛求得两个子问题的upper bound为Z_LP1 = 12.75，Z_LP2 = 12.2。由于Z_LP1 和Z_LP2都大于BestV=-INF，说明这两支均满足要求。继续往下。

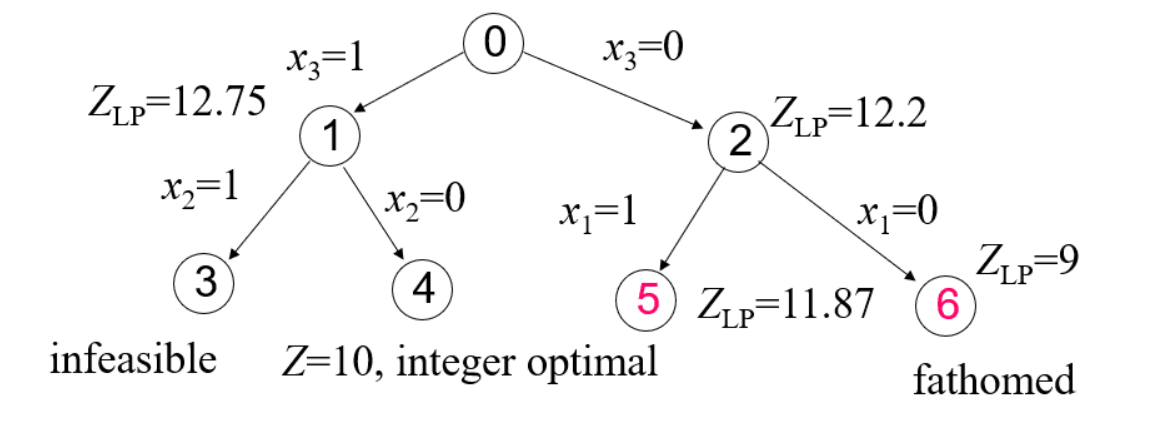
  1. 从节点 1 和节点 2 两个子问题再次分支，得到如下结果
image-20220412161353856

子问题3已经不可行，无需再理。子问题4通过线性松弛得到最优解为10，刚好也符合原问题0的所有约束，在该支找到一个可行解，更新BestV = 10。

子问题5通过线性松弛得到upper bound为11.87>当前的BestV = 10，因此子问题5还有戏，待下一次分支。而子问题6得到upper bound为9<当前的BestV = 10，那么从该支下去找到的解也不会变得更好，所以剪掉！

  1. 对结点5进行分支
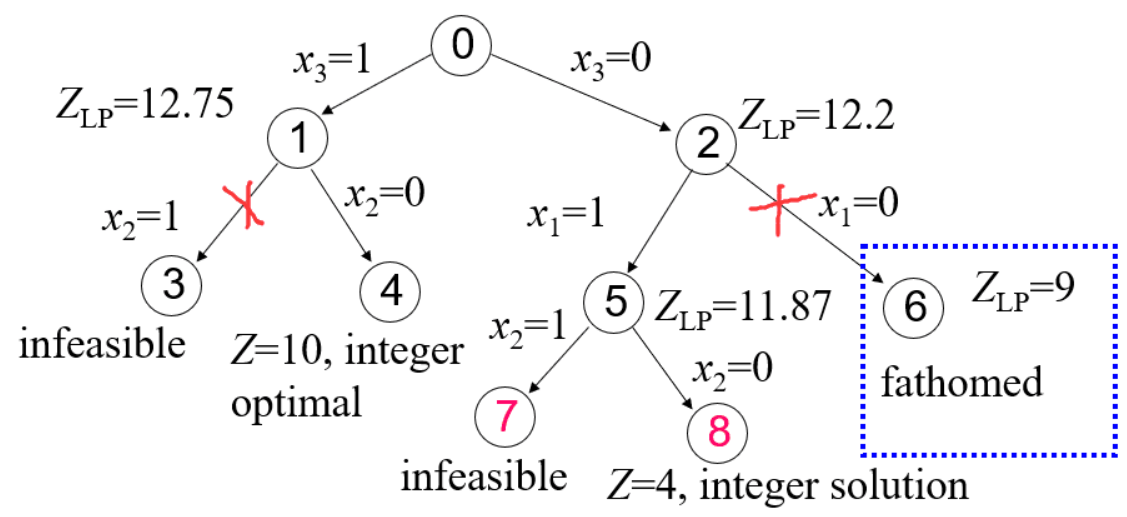
image-20220412161453040

子问题7不可行，无需再理。子问题8得到一个满足原问题0所有约束的解，但是目标值为4<当前的BestV=10，所以不更新BestV，同时该支下去也不能得到更好的解了。

  1. 此时，所有的分支遍历都完成，我们最终找到了最优解。

分支定界法（branch and bound）是一种求解整数规划问题的最常用算法。这种方法不但可以求解纯整数规划，还可以求解混合整数规划问题。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
1. Using a heuristic, find a solution xh to the optimization problem. Store its value, B = f(x_h). (If no heuristic is available, set B to infinity.) B will denote the best solution found so far, and will be used as an upper bound on candidate solutions.

2. Initialize a queue to hold a partial solution with none of the variables of the problem assigned.

3. Loop until the queue is empty:

	3.1. Take a node N off the queue.
	
	3.2. If N represents a single candidate solution x and f(x) < B, then x is the best solution so far. Record it and set B ← f(x).
	
	3.3. Else, branch on N to produce new nodes Ni. For each of these:

		3.3.1. If bound(N_i) > B, do nothing; since the lower bound on this node is greater than the upper bound of the problem, it will never lead to the optimal solution, and can be discarded.
		
		3.3.2. Else, store Ni on the queue.

ref: https://www.cnblogs.com/dengfaheng/p/11225612.html

branch and cut

branch and cut其实还是和branch and bound脱离不了干系的。

在应用branch and bound求解整数规划问题的时候，如下图:

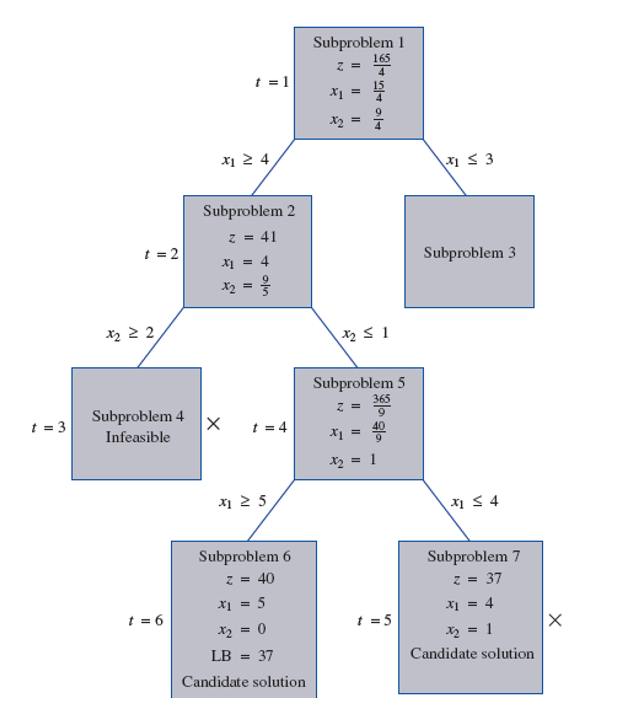
image-20220412171138059

假如，我们现在求一个整数规划最大化问题，在分支定界过程中，求解整数规划模型的LP松弛模型得到的非整数解作为上界，而此前找到的整数解作为下界。 如果出现某个节点upper bound低于现有的lower bound，则可以剪掉该节点。否则，如果不是整数解继续分支。

此外，在求解整数规划模型的LP松弛时，If cutting planes are used to tighten LP relaxations。那么这时候的branch and bound就变成了branch and cut。 割平面

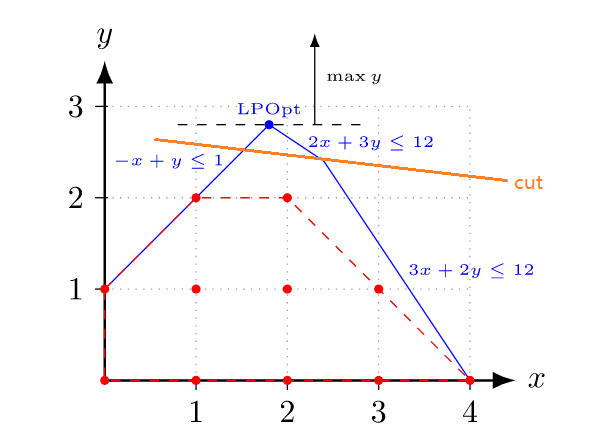
image-20220412171238809

红色部分是整数规划的可行解空间。
蓝色部分是整数规划的LP松弛可行解空间。
在求解LP松弛时，加入橙色的cut，缩小解空间，同时又不影响整数解的解空间，可使解收敛得更快。

这就是branch and cut的过程了。比branch and bound高明之处就在于多了一个cutting planes，可能使branch and bound的效率变得更高。

例子
$$
min~~~~~~~~~~~~~ &z=-6x_1-5_2 \
subject~to~~~&3x_1+x_2 \leq 11 \
&-x_1+2x_2 \leq 5 \
&x_1,x_2 \geq 0
$$
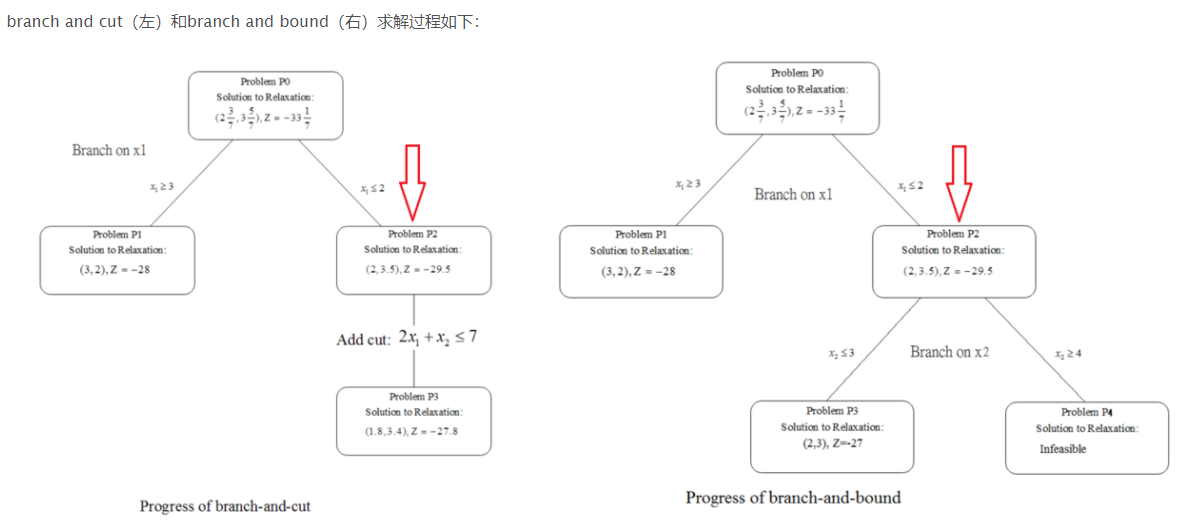
image-20220412171533780

image-20220412171629952

ref: https://www.cnblogs.com/dengfaheng/p/11344488.html

更加详细的一个参考：https://zhuanlan.zhihu.com/p/28387290?group_id=893712252413284352

内点法

各类梯度下降法和牛顿法

批量梯度下降：

  1. 是最小化所有样本的损失函数，最终得到全局最优解。　　　　　　

  2. 由于每次更新参数需要重新训练一次全部的样本，代价比较大，适用于小规模样本训练的情况。

随机梯度下降：

  1. 是最优化每个样本的损失函数。每一次迭代得到的损失函数不是，每次每次向着全局最优的方向，但是大体是向着全局最优，最终的结果往往是在最优解的附近。　　　

  2. 当目标函数是凸函数的时候，结果一定是全局最优解。

    　　　　　　　3. 适合大规模样本训练的情况。

小批量梯度下降法：

　将上述两种方法作结合。每次利用一小部分数据更新迭代参数。即样本在1和m之间。

牛顿法：

是通过求解目标函数的一阶导数为0时的参数，进而求出目标函数最小值时的参数。

优点：收敛速度很快。海森矩阵的逆在迭代过程中不断减小，可以起到逐步减小步长的效果。

缺点：海森矩阵的逆计算复杂，代价比较大，因此有了拟牛顿法。

x多变量时，二阶导使用hessian 矩阵

梯度下降法：

是通过梯度方向和步长，直接求解目标函数的最小值时的参数。

越接近最优值时，步长应该不断减小，否则会在最优值附近来回震荡。

image-20220405211558700 image-20220405211627441 image-20220405211655906 image-20220405211707643 image-20220405211722098

使用牛顿法/拟牛顿法收敛更快。但是每次迭代的时间比梯度下降法长。

ref: https://zhuanlan.zhihu.com/p/112416130

CO

MIP

MILP

非线性转为线性

基于CO，CO做了有功和无功的平衡

将约束条件转换为惩罚项。使得主问题变为线性问题，求解MILP

RO

苏文藻课程

SO

苏文藻课程

distributionally robust optimization

苏文藻课程

粒子群算法（PSO）和遗传算法

PSO: partivcle swarm optimizatioin

GA: genetic algorithm

PSO和GA的相同点：

  1. 都属于仿生算法。PSO主要模拟鸟类觅食、人类认知等社会行为而提出；GA主要借用生物进化论中”适者生存“的规律。
  2. 都属于全局优化方法。两种算法都是在解空间随机产生初始种群，因为算法在全局的解空间进行搜索，且将搜索重点集中在性能高的部分。
  3. 都属于随机搜索算法。都是通过随机优化方法更新种群和搜索最优点。PSO中认知项和社会项前都加有随机数。GA的遗传操作均属于随即操作。
  4. 都隐含并行性。搜索过程是从问题解的一个集合开始，而不是从单个个体开始，具有隐含并行搜索特性，从而减小了陷入局部极小的可能性。
  5. 根据个体的适配信息进行搜索，因此不受函数约束条件的限制，如连续性、可导性等。
  6. 对高维复杂问题，往往会遇到早熟收敛和收敛性能差的缺点，都无法保证收敛到最优点。

PSO和GA的不同点：

  1. PSO有记忆，好的解的所有粒子均保存，而GA没有记忆，以前的知识随着种群的改变而被破坏。
  2. GA算法中，染色体之间相互共享信息，所以整个种群的移动是比较均匀的向最优区域移动。PSO中的例子仅仅通过当前搜索到的最优点进行共享信息，所以很大程度上这是一种单项信息共享机制，整个搜索更新过程是跟随当前最优解的过程。在大多数情况下，所有粒子可能比遗传算法中的进化个体以更快速度收敛于最优解。
  3. PSO相对于GA，不需要编码，没有交叉和变异操作，粒子只是通过内部速度进行更新，因此原理更简单、参数更少、实现更容易。
  4. PSO算法主要应用于连续问题，包括神经网络训练和函数优化等，而GA除了连续问题之外，还可应用于离散问题，比如TSP问题、货郎担问题、工作车间调度等。

禁忌搜索算法

禁忌搜索(Tabu Search, TS)也是属于模拟人类智能的一种优化算法。

img

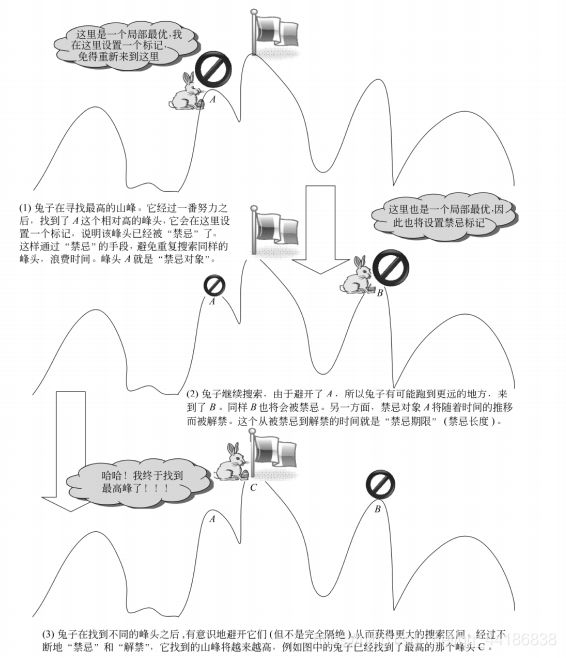
禁忌表（Tabu List，TL）
是用来存放（记忆）禁忌对象的表。它是禁忌搜索得以进行的基本前提。禁忌表本身是有容量限制的，它的大小对存放禁忌对象的个数有影响，会影响算法的性能。

禁忌对象（Tabu Object，TO）
是指禁忌表中被禁的那些变化元素。禁忌对象的选择可以根据具体问题而制定。例如在旅行商问题（Traveling Salesman Problem，TSP）中可以将交换的城市对作为禁忌对象，也可以将总路径长度作为禁忌对象。

禁忌期限（Tabu Tenure，TT）
也叫禁忌长度，指的是禁忌对象不能被选取的周期。禁忌期限过短容易出现循环，跳不出局部最优，长度过长会造成计算时间过长。

渴望准则（Aspiration Criteria，AC）
也称为特赦规则。当所有的对象都被禁忌之后，可以让其中性能最好的被禁忌对象解禁，或者当某个对象解禁会带来目标值的很大改进时，也可以使用特赦规则。

非对称的旅行商问题（ATSP）

image-20220415155952005

分析：这是一个简单的问题,利用枚举的方法也可以找到最优的答案，但是，找到答案不是我们的目的，我们主要是想通过一一个简单的例子来理解禁忌搜索是如何进行工作的。从距离矩阵D可以看到，这是一个非对称的TSP问题，但是这并不影响算法的执行。由于题目假设了邻域构造的方式，而且规定了始点和终点都是城市a，因此，在以下的求解过程中，我们不使用城市a和其他城市进行交换，这样的操作并不会影响全局寻优的能力。

img

注：在实际应用中，通过选择更高的禁忌对象，设置合理的禁忌期限，或者采用其他更好的的参数，都可以避免循环（反复出现同种情况的邻域值）的出现，提高算法的性能。

常见的机器学习算法

SVM

43E6AF2BAF69572D95CD2DBEAECD8CB2 IMG_0397 IMG_0399

IMG_0400

QQ图片20220404232547

机器学习给的KKT和凸优化给的不同。但是我认为二者是等价的，应该可以互推。

这个是凸优化上的条件。

image-20220405110624726

贝叶斯

后验概率的获得主要有两种策略

  1. 给定x，直接建模$P(c|x)$来预测c，这样叫做”判别式模型“
  2. 先对联合概率分布$P(x|c)$建模，然后再由此获得$P(c|x)$.

$$
P(c|x)&= \frac{P(cx)}{P(x)} =\frac{P(c)P(x|c)}{P(x)} \
&=\frac{P(c)}{P(x)}\cdot\frac{P(x|c)}{P(x)}\
&= \frac{P(c)}{P(x)}\cdot \prod_{i=1}^{d}P(x_i|c)
$$

$P(cx) = P(c)P(x|c) = P(x)P(x|c)$

朴素贝叶斯要求独立同分布。

半朴素贝叶斯分类器，对属性条件独立性假设进行了一定程度的放松。

IMG_0408

贝叶斯网，借助有向无环图来刻画属性之间的依赖关系。用条件概率表来描述属性的联合概率分布。

EM算法

我们一直假设训练样本的所有属性都被观测到，即训练样本是完整的，但是现实中常遇到不完整的样本，这种未能观测到的特征称为”隐变量“。

令X表示已观测到的变量集，Z表示隐变量集，$\Theta$表示模型参数，若欲对$\Theta$做极大似然估计，则应该最大化对数似然。
$$
LL(\Theta|X,Z) = \ln P(X,Z|\Theta)
$$
由于Z是隐变量，该式无法求解，此时可以通过对Z计算期望，来最大化已观测数据的对数”边际似然“

IMG_0406 image-20220405163218219 image-20220405163353314 image-20220405163644044 IMG_0407 image-20220405164448434 image-20220405170825391

$\propto$正比于

image-20220405171059473

Linear model

HMM

隐马尔科夫模型是结构最简单的动态贝叶斯网，是一种著名的有向图模型，主要用于时序数据建模，在语音识别、自然语言处理等领域有广泛应用。

三个基本步骤

  1. 给定参数，观测序列，计算条件概率

  2. 参数学习，给定序列，反推参数

  3. 解码。给定参数和观测序列，求最大可能性。

次梯度

支撑超平面的斜率就是次梯度。

最起码是凸函数才能保证任意一点的次梯度存在。

次梯度下降

image-20220405135334199

近端梯度

image-20220405150019553

image-20220405150032359

image-20220405150045008

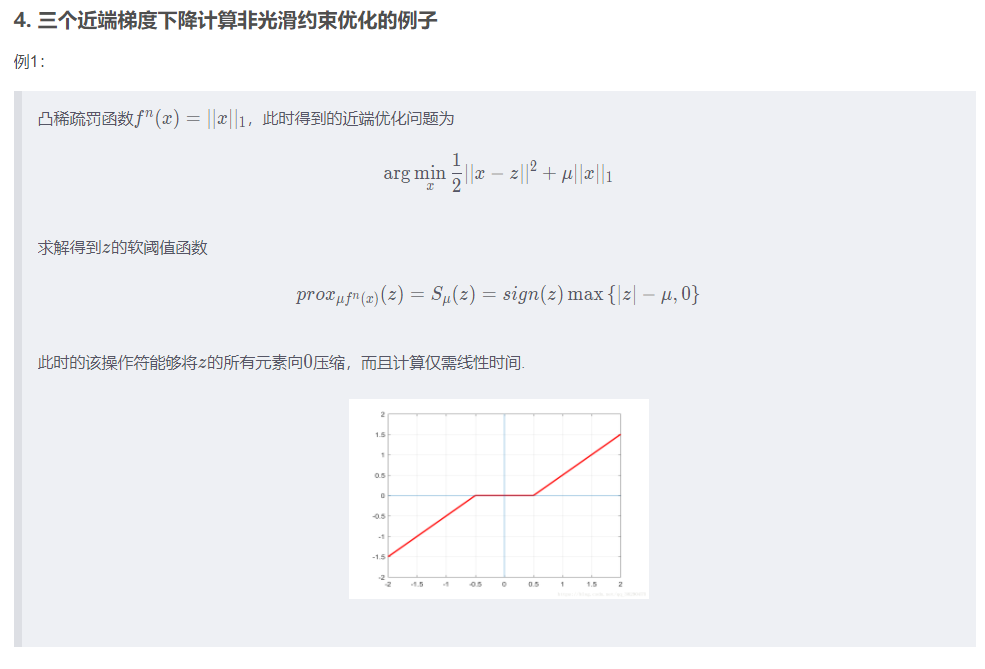
image-20220405150056680

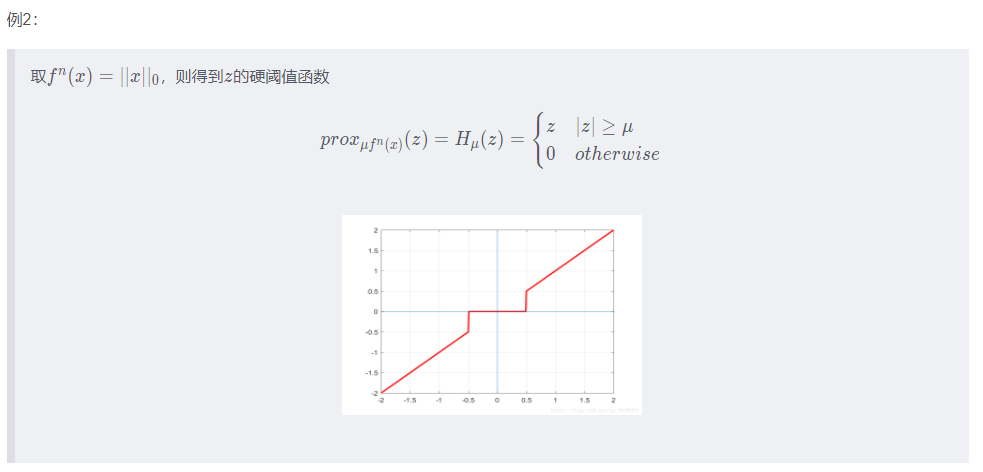
image-20220405150213656

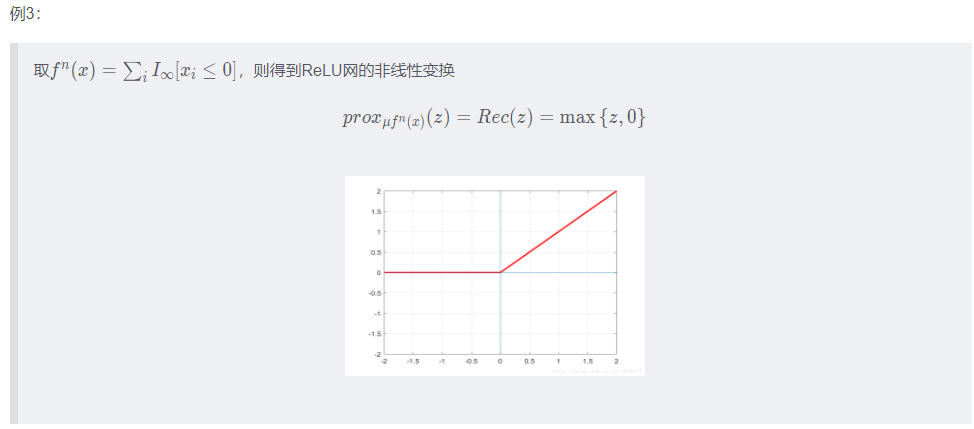
image-20220405150221222

ref：https://blog.csdn.net/qq_38290475/article/details/81052206

特征工程

img

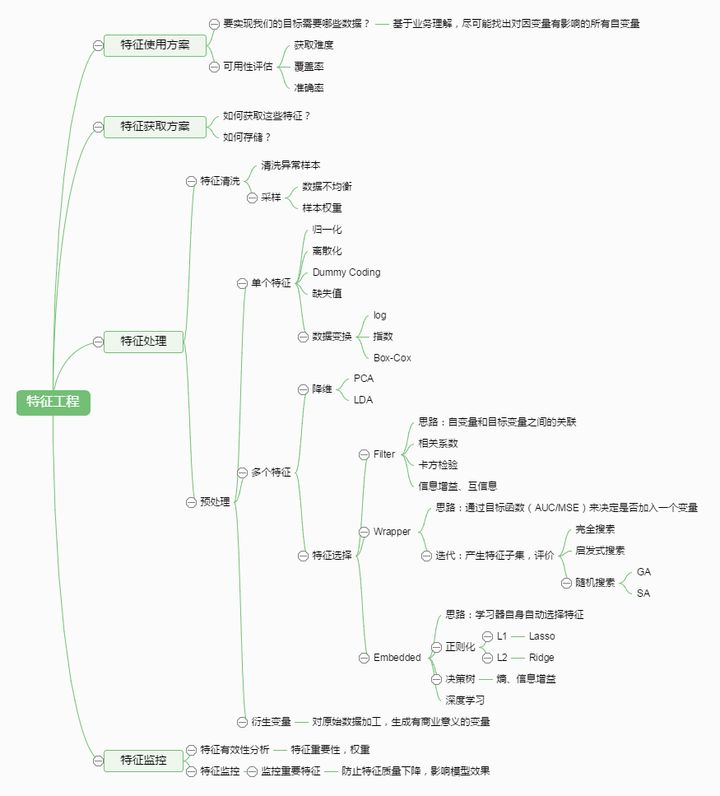
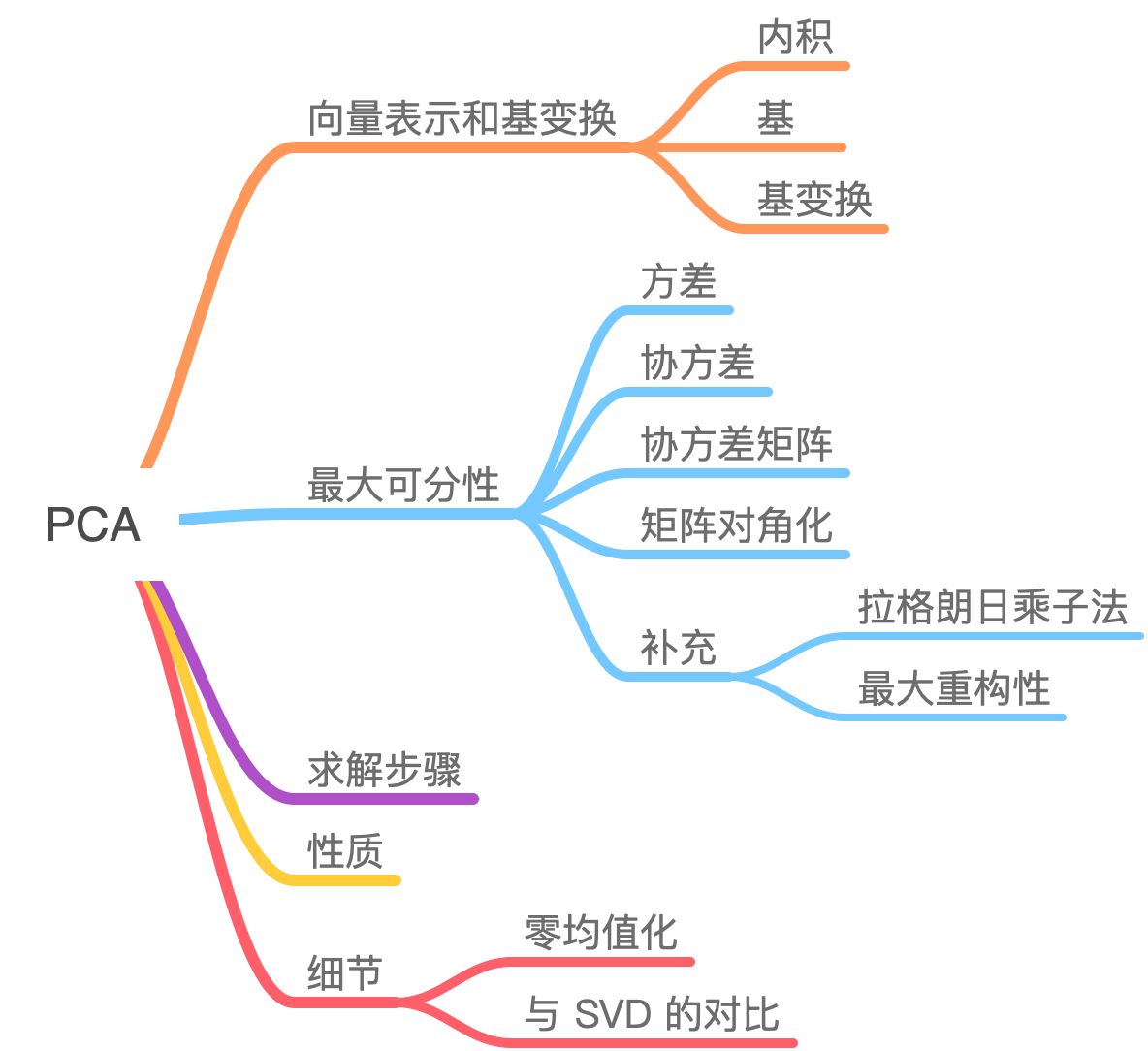
PCA

【机器学习】降维——PCA（非常详细）

风电数据

构建DRO时候，不同机组的历史数据不同，

img

LDR变换

pickup and delivery problem with time-windows

求解PDPTW问题的算法包括：列生成算法（column generation）、分支切割（branch-and-cut）、分支切割定价（branch-and-cut-and-price）等精确计算算法，禁忌搜索（tabu search）、模拟退火（simulated annealing algorithm）、基于插入搜索的算法（insertion-based heuristic）、自适应大邻域搜索（adaptive large neighborhood search）、变深度搜索（variable-depth search algorithm）。由于在配送场景下，对算法时效性有极高的要求，上述算法均无法适用于配送场景的问题。在后文中，我们将介绍路径规划的问题模型，以及提出的启发式算法（Two-Stage Fast Heuristic），同时给出了一些仿真结果。

ref: https://segmentfault.com/a/1190000024516742

指派问题(Assignment Problems - AP)

https://blog.csdn.net/qq_38361726/article/details/120738776

车辆路径问题(VRP)

VRP是指一定数量的客户，各自有不同数量的货物需求，配送中心向客户提供货物，由一个车队负责分送货物，组织适当的行车路线，目标是使得客户的需求得到满足，并能在一定的约束下，达到诸如路程最短、成本最小、耗费时间最少等目的。

TSP是VRP问题的特例。

旅行商问题(TSP)

img

img

其中约束(3)尽管可被简化但仍使得该问题成为了NP问题，因此基于上述讨论，本文将简单介绍可用于解决TSP的启发式算法。

非对称旅行商问题（ATSP）

非对称旅行商问题（STSP）

凸包算法

Graham scan

image-20220423094807908