剑指offer回忆录

发表于 更新于

链表

从尾到头打印链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
1. 栈
2. insert
3.递归

class Solution {
  public:
    void backtrace(vector<int>& vec, ListNode* p){
        if(p->next){
            backtrace(vec, p->next);
        }
        vec.push_back(p->val);
    }
    
    vector<int> printListFromTailToHead(ListNode* head) {
        vector<int> vec;
        if(head == nullptr){
            return vec;
        }       
        backtrace(vec, head);
        return vec;
    }
};

在vector对象尾部之外的位置插入或删除元素可能很慢，那么结合链表与顺序表的特性可以认为vector对象的元素所使用的数据结构应该是顺序表。

反转链表

1
2
3
4
5
6
7
8
9
10
ListNode* ReverseList(ListNode* pHead) {  //头插法反转
        ListNode* newHead = new ListNode(-1); //新的头节点
        while(pHead != nullptr){
            ListNode* nxt = pHead->next;  //提前保存head的下一个结点，防止赋值后head更改
            pHead->next = newHead->next;
            newHead->next = pHead;
            pHead = nxt;
        }
        return newHead->next;
    }

合并两个排序的链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
ListNode* Merge(ListNode* pHead1, ListNode* pHead2) {
        if(pHead1 == nullptr){
            return pHead2;
        }
        if(pHead2 == nullptr){
            return pHead1;
        }
        // 节省空间就不创建新的链表了，较小的当第一个节点
        ListNode *nh = pHead1->val <= pHead2->val?pHead1:pHead2;
        ListNode *prev = nh; // 尾结点
        ListNode *nxt = nullptr; // temp
        while(pHead1 && pHead2){
            if(pHead1->val <= pHead2->val){
                nxt = pHead1;
                pHead1 = pHead1->next;
            }else{
                nxt = pHead2;
                pHead2 = pHead2->next;
            }
            prev->next = nxt;
            prev = prev->next;
        }
        
        while(pHead1){
            prev->next = pHead1;
            prev = prev->next;
            pHead1 = pHead1->next;
        }
        
        while(pHead2){
            prev->next = pHead2;
            prev = prev->next;
            pHead2 = pHead2->next;
            
        }
        prev->next = nullptr;
        return nh;
    }

复杂链表的复制

每个节点中有节点值，以及两个指针，一个指向下一个节点，另一个特殊指针random指向一个随机节点。对此链表进行深拷贝。

浅拷贝：又称值拷贝，将源对象的值拷贝到目标对象中去，本质上来说源对象和目标对象共用一份实体，只是所引用的变量名不同，地址其实还是相同的。

深拷贝：拷贝的时候先开辟出和源对象大小一样的空间，然后将源对象里的内容拷贝到目标对象中去，这样两个指针就指向了不同的内存位置。并且里面的内容是一样的，这样不但达到了我们想要的目的，还不会出现问题，两个指针先后去调用析构函数，分别释放自己所指向的位置。即为每次增加一个指针，便申请一块新的内存，并让这个指针指向新的内存，深拷贝情况下，不会出现重复释放同一块内存的错误。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
/*
struct RandomListNode {
    int label;
    struct RandomListNode *next, *random;
    RandomListNode(int x) :
            label(x), next(NULL), random(NULL) {
    }
};
*/
class Solution {
public:
    RandomListNode* Clone(RandomListNode* pHead) {
        // 先拷贝原链表
        RandomListNode* pre = new RandomListNode(-1);
        RandomListNode* last = pre, * p = pHead;
        unordered_map<RandomListNode*, RandomListNode*> mp;
        while(p){
            RandomListNode* new_node = new RandomListNode(p->label);
            mp[p] = new_node;  // 旧结点对应的新结点
            last->next = new_node;
            p=p->next;
            last = last->next;
        }
        
        for(auto& [key, value]:mp){
            // key 旧结点    value为新结点
            value->random = key->random == nullptr ? nullptr:mp[key->random];
        }
        return pre->next;
    }
};

排序的循环链表

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
/*
// Definition for a Node.
class Node {
public:
    int val;
    Node* next;

    Node() {}

    Node(int _val) {
        val = _val;
        next = NULL;
    }

    Node(int _val, Node* _next) {
        val = _val;
        next = _next;
    }
};
*/

class Solution {
public:
    Node* insert(Node* head, int insertVal) {
        Node* node = new Node(insertVal);
        if(head == nullptr){
            node->next = node;
            return node;
        }
        // 1个
        if(head->next == head){
            head->next = node;
            node->next = head;
            return head;
        }
        Node* cur = head;
        Node* nxt = head->next;
        while(nxt!=head){
            if(insertVal>=cur->val && insertVal <= nxt->val){  //  正常递增
                break;
            }
            if(cur->val > nxt->val){  // nxt已经到了最小元素
                if(insertVal > cur->val || insertVal < nxt->val){
                    // insertVal > cur->val 说明 insertval是最大值  3 5 1  插入值为6  结果为 3561
                    // insertVal < nxt->val 说明 insertval是最小值  3 5 1  插入值为0  结果为 3501
                    // 这两种情况都可以插入在 5 和 1 之间
                    break;
                }
            }
            cur = nxt;
            nxt = nxt->next;
        }
        cur->next = node;
        node->next = nxt;
        return head;
    }
};

树

树的子结构

判断一棵树是不是另一棵树的子结构.

没啥好解释的，我直接暴力穷举。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
class Solution {
public:
    bool HasSubtree(TreeNode* pRoot1, TreeNode* pRoot2) {
        if(!pRoot1 || !pRoot2){
            return false;
        }
        
        std::function<bool(TreeNode*, TreeNode*)> compareVal = [&](TreeNode* p, TreeNode* q)->bool{
            if(q == nullptr){
                return true;
            }
           
            if(p == nullptr || p->val != q->val){
                return false;
            }
            return compareVal(p->left, q->left) && compareVal(p->right,q->right);
        };
        bool tag = false;
        queue<TreeNode*> que;
        que.push(pRoot1);
        while(!que.empty()){
            auto temp = que.front();
            que.pop();
            tag = compareVal(temp, pRoot2);
            if(tag){
                return true;
            }
            if(temp->left){
                que.push(temp->left);
            }
            if(temp->right){
                que.push(temp->right);
            }
        }
        return false;
    }
};

二叉树的镜像

我第一反应想的是层次遍历倒序

发现前序，中序获得，倒序构建貌似也可以。没实验过

递归操作也可以用

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
TreeNode* Mirror(TreeNode* pRoot) {   // 递归
        if(pRoot == nullptr){
            return nullptr;
        }
        if(!pRoot->left && !pRoot->right){
            return pRoot;  // 单节点返回自身, {1} return 1;
        }
        TreeNode* temp = pRoot->left;
        pRoot->left = pRoot->right;
        pRoot->right = temp;
        Mirror(pRoot->left);
        Mirror(pRoot->right);
        
        return pRoot;
    }

对称的二叉树

判断二叉树是否对称。

中序遍历拆开 或者 不拆开直接判断，即递归，一样的。

非递归方法，使用stack，每次成双取出，判断p1->left == p2->right && p1->right == p2->left。然后成双放入。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
bool isSymmetrical(TreeNode* pRoot) {
        if(pRoot == nullptr || (!pRoot->left && !pRoot->right)){
            return true;
        }
        
        std::function<bool(TreeNode*, TreeNode*)> cpr = [&](TreeNode* leftt, TreeNode* rightt)->bool{
            if(leftt == nullptr && rightt == nullptr){
                return true;
            }
            // 说明不全空
            if(leftt==nullptr || rightt == nullptr){
                return false;  //一空一不空
            }
            return leftt->val == rightt->val
                   && cpr(leftt->right, rightt->left)
                   && cpr(leftt->left, rightt->right);
        };
        
        return cpr(pRoot->left, pRoot->right);
    }

边界条件处我犯了错。状态判断不好。

从上往下打印二叉树

层次遍历。不赘述

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
vector<int> PrintFromTopToBottom(TreeNode* root) {
        vector<int> ans;
        if(root == nullptr){
            return ans;
        }
        queue<TreeNode*> que;
        que.push(root);
        while(!que.empty()){
            TreeNode* temp = que.front();
            ans.push_back(temp->val);
            que.pop();
            if(temp->left){
                que.push(temp->left);
            }
            if(temp->right){
                que.push(temp->right);
            }
            
        }
        return ans;
    }

二叉搜索树的后序遍历序列

二叉搜索树的中序遍历是递增的。

后序遍历的最后一位是根节点root

说明序列中，小于root->val的都是左子树，大于的都是右子树

接下来，相似的操作。

如 2 4 3 6 8 7 5 -> root = 5 left: 2 4 3 right: 6 8 7

2 4 3 -> root=3 left = 2 right = 4 6 8 7 -> root = 7 left = 6 right = 8

递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
bool VerifySquenceOfBST(vector<int> sequence) {
       std::function<bool(vector<int>&, size_t, size_t)> judge = 
           [&](vector<int>& seq, size_t l, size_t r)->bool{
           if(l >= r){
               return true;
           }
           int temp = seq[r];  // root
           int i = r - 1;
           while(i>l && seq[i]>temp){
               --i;
           }
           //找到分界点了
           // 判断左侧是否全部都是小于temp的
           for(size_t j = l;j<i;++j){
               if(seq[j]>temp){
                   return false;
               }
           }
           
           return judge(seq, l, i) && judge(seq, i+1, r-1);
       };
        if(sequence.empty()){
            return false;
        }
        size_t n = sequence.size();
        return judge(sequence, 0, n-1);
        
    }

二叉树中和为某一值的路径(二)

找出二叉树中结点值的和为目标值的所有路径（路径指根节点到叶子）

可以及时剪枝。

先序遍历的做法来遍历。

考虑负数！负数的话，大于的判断符号就没法使用

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
class Solution {
private:
    int expect;    
public:
    vector<vector<int>> FindPath(TreeNode* root,int expectNumber) {
        vector<vector<int>> ans;
        if(root == nullptr){
            return ans;
        }
        this->expect = expectNumber;
        
        std::function<void(TreeNode*, int, vector<int>, vector<vector<int>>&)> dfs = 
            [&](TreeNode* rt, int sum,vector<int> temp, vector<vector<int>>& ans) -> void{
            if(rt == nullptr){
                return;
            }
            sum+=rt->val;
            temp.push_back(rt->val);
            if(sum == expect && rt->left == nullptr && rt->right == nullptr){
                ans.push_back(temp);
                temp.clear();
                return;
            }
            // <
            if(rt->left)
                dfs(rt->left, sum, temp, ans);
            if(rt->right)
                dfs(rt->right, sum, temp, ans);
            temp.pop_back();
        };
        
        vector<int> temp;
        dfs(root, 0, temp, ans);
        return ans;
    }
};

二叉搜索树与双向链表

输入一棵二叉搜索树，将该二叉搜索树转换成一个排序的双向链表。

方法一：直接中序重新构造

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
/*
struct TreeNode {
	int val;
	struct TreeNode *left;
	struct TreeNode *right;
	TreeNode(int x) :
			val(x), left(NULL), right(NULL) {
	}
};*/
class Solution {
public:
    TreeNode* Convert(TreeNode* pRootOfTree) {
        if(pRootOfTree == nullptr){
            return pRootOfTree;
        }
        std::function<void(TreeNode*, TreeNode*&)> trans = [&](TreeNode* root, TreeNode*& last)->void{
            if(root == nullptr){
                return;
            }
            if(root->left){
                trans(root->left, last);
            }
            last->right = root;
            root->left = last;
            last = root;
            if(root->right){
                trans(root->right, last);
            }
            return;
        };
        
        TreeNode* p = new TreeNode(-1);
        TreeNode* q = p;
        trans(pRootOfTree, q);
        p=p->right;
        p->left = nullptr;
        return p;
    }
};

方法二：不开辟新的结点，直接在原节点操作。这就需要保存中序遍历过程中的前继结点。给个全局变量，保存前继。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
/*
struct TreeNode {
	int val;
	struct TreeNode *left;
	struct TreeNode *right;
	TreeNode(int x) :
			val(x), left(NULL), right(NULL) {
	}
};*/
class Solution {
public:
    TreeNode* preNode;  // 前驱结点
    TreeNode* Convert(TreeNode* pRootOfTree) {
        // 先找到preNode
        if(pRootOfTree == nullptr){
            return pRootOfTree;
        }
        
        std::function<void(TreeNode*)> trans = [&](TreeNode* root)->void{
            if(root == nullptr) {
            return;
        }
        trans(root->left);  //走到起始点
            // 找到最左侧，此时root == p
        root->left = preNode;
        preNode->right = root;
        preNode = root;    
        trans(root->right);
        };

        TreeNode* p = pRootOfTree;
        while(p->left){
            p = p->left;  // 链表的起始节点
        }
        preNode = new TreeNode(-1);
        trans(pRootOfTree);
        p->left = nullptr;
        return p;  // 链表的头
    }

};

序列化二叉树

请实现两个函数，分别用来序列化和反序列化二叉树，不对序列化之后的字符串进行约束，但要求能够根据序列化之后的字符串重新构造出一棵与原二叉树相同的树。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
class Codec {
public:
	struct TreeNode {
		int val;
		TreeNode* left;
		TreeNode* right;
		TreeNode(int x) : val(x), left(NULL), right(NULL) {}
	};

	// Encodes a tree to a single string.
	string serialize(TreeNode* root) {
		string res = "";
		TreeNode* p = root;
		preOrder(p, res);
		// 使用递归，把最后一个逗号删除
		res.pop_back();

		// 使用迭代，最后还少个"X"
		// preOrder_case2(p, res);
		// res += "X";

		return res;
	}

	// 使用递归方式
	void preOrder(TreeNode* root, string& str) {
		if (root == nullptr) {
			str += "X";
			str += ",";
			return;
		}
		str += to_string(root->val);
		str += ",";
		preOrder(root->left, str);
		preOrder(root->right, str);
	}

	// 使用 非递归方式 进行前序遍历
	void preOrder_case2(TreeNode* root, string& str) {
		stack<TreeNode*> st;
		st.push(root);
		str = str + to_string(root->left->val) + ",";
		TreeNode* temp = root;
		int visited_node = 0;
		while (temp!= nullptr || !st.empty()) {
			if (temp!=nullptr) {  // 一直向左走
				st.push(temp);
				str += to_string(temp->val);   // 不断保存经过的结点
				str += ",";
				temp = temp->left;  // 走到最左
			}
			else { // 找右子树
				str += "X";   // 不断保存经过的结点
				str += ",";
				temp = st.top();  // 回溯到父结点
				st.pop();
				temp = temp->right;
				
			}
		}
	}


	// Decodes your encoded data to tree.
	TreeNode* deserialize(string data) {  // 只给了一个string ，说明不能通过 前/中 + 后序  来确定唯一的二叉树
		deque<string> que;
		stringstream ss;
		string temp;
		ss << data;
		while (getline(ss, temp, ',')) {
			que.push_back(temp);
		}
		// 按照 ’,‘ 分割好了
		return anls(que);
	}

	// 从左到右解析字符串
	TreeNode* anls(deque<string>& que) {
		// que 从前往后
		if (!que.empty() && que.front() == "X") {  // 为空结点
			que.pop_front();
			return nullptr;
		}
		auto temp = new TreeNode(stoi(que.front()));
		que.pop_front();
		temp->left = anls(que);
		temp->right = anls(que);
		return temp;
	}
};

删除二叉搜索树中的节点

leetcode450

难点主要在于删除操作

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class Solution {
public:
    // cur的左右节点都为空，cur可以直接删除
    // 右节点为空，找左节点的最大值
    // 左节点为空，找右节点的最小值
    // 左右节点均不为空，那么去左边找最大值或右边找最小值都可以,来替换掉cur
    // 解法可以看作不断地重构二叉搜索树(BST)
    TreeNode* deleteNode(TreeNode* root, int key) {
        if(root == nullptr){
            return nullptr;
        }
        if(root->val < key){
            root->right = deleteNode(root->right, key);
            return root;
        }
        if(root->val> key){
            root->left = deleteNode(root->left,key);
            return root;
        }
        if(root->val==key){  // ==
            if(root->left == nullptr && root->right == nullptr){
                // 直接删除root
                return nullptr;
            }
            if(root->right == nullptr){  // 右空，找左边最大值,刚好是左边第一个
                return root->left;
            }
            if(root->left == nullptr){ // 左空，找右边最小值，刚好是右边第一个
                return root->right;
            }
            // 两侧都不为空
            // 这里找右边最小值，换掉root
            TreeNode* rep = root->right;
            // 如果右边第一个有左子树，那么就一直找,因为最小值如果在左子树，那么肯定在第一个结点的左子树
            while(rep->left!=nullptr){
                rep = rep->left;
            }
            // 此时已经找到最小值的结点了
            // 重构需要删除结点的右子树， 值要根据rep（即替换节点的值重构
            root->right = deleteNode(root->right, rep->val);
            // 把这个结点替换掉需要删除的结点 root
            rep->right = root->right;
            rep->left = root->left;
            return rep;
        }
        return root;
    }
};

排序

最小的K个数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
// 长度为 n 的可能有重复值的数组，找出其中不去重的最小的 k 个数
// [0,1,2,1,2],3    ->   [0,1,1]
/*
* case1  直接排序取前K
* case2  容量为K的优先队列(大顶堆)。 小于则进去且弹出堆顶
* case3  topK算法
*/

// case1略


// case2







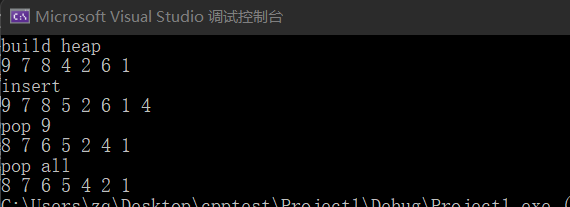
（大顶）堆的建立，插入，删除

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
class HeapBID {
public:
	// 数组下标从0开始
	void shiftDown(vector<int>& nums, int k) {  // 向下调整
		int leftChild = k * 2 + 1, rightChild = k * 2 + 2;
		int maxIndex = k; //假设在当前节点，及其左、右子节点，共三个节点中，最大的是当前这个节点。后序我们就要更新max，看到底哪个才是最大的，把最大的那个和当前节点交换
		if (leftChild < nums.size() && nums[leftChild] > nums[maxIndex])
			maxIndex = leftChild;
		if (rightChild < nums.size() && nums[rightChild] > nums[maxIndex])
			maxIndex = rightChild;
		if (maxIndex != k)
		{
			swap(nums[maxIndex], nums[k]);
			shiftDown(nums, maxIndex); // 如果原k节点调整了位置(上一步swap调整)，那么就要将k继续做shiftDown操作，直到它比它的左、右孩子都大
		}
		
	}
	//  建立的是大顶堆
	// 向上调整，删除堆顶时候使用
	void shiftUp(vector<int>& nums) {  // 向上调整
		// 首先将最后一个孩子节点插入到头节点
		int child = nums.size() - 1;
		int parent = (child - 1) / 2;
		while (child > 0) {
			if (nums[parent] < nums[child]) {
				swap(nums[parent], nums[child]);
			}
			else {
				break;
			}
			child = parent;
			parent = (child - 1) / 2;  // 换层
		}
	}

	void buildMaxHeap(vector<int>& nums) {
		int n = nums.size();
		for (int i = 0; i < n/2; ++i) {  // 从第一个非叶子节点开始，从下往上，将每棵子树调整成最大堆
			shiftDown(nums, i);
		}
	}

	void inHeap(vector<int>& nums, int x) {
		nums.push_back(x);
		shiftUp(nums);
	}

	void pollHeap(vector<int>& nums) {
		int oldVal = nums[0]; // 头元素
		nums[0] = nums[nums.size() - 1];
		nums.pop_back(); // 弹出末尾
		shiftDown(nums, 0);
	}
};


/**/
int main() {
	vector<int> nums{ 1,4,9,7,2,6,8 };
	HeapBID h;
	h.buildMaxHeap(nums);
	cout << "build heap" << endl;
	for (auto& a : nums) {
		cout << a << " ";
	}
	cout << endl;
	cout << "insert" << endl;
	h.inHeap(nums,5);
	for (auto& a : nums) {
		cout << a << " ";
	}

	cout << endl;
	cout << "pop " << nums[0] << endl;
	h.pollHeap(nums);
	for (auto& a : nums) {
		cout << a << " ";
	}

	cout << endl;
	cout << "pop all" << endl;
	int n = nums.size();
	for (int i = 0; i < n; ++i) {
		cout << nums[0] << " ";
		h.pollHeap(nums);
	}
	return 0;
}
image-20220602224323732

位运算

模拟

顺时针打印矩阵

从外向里以顺时针打印。

螺旋输出，小心单行的情况，要判断 if (top != bottom) 和 if (left != right)

在这里犯了错。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
vector<int> printMatrix(vector<vector<int> > matrix) {
        int m = matrix.size();
        int n = matrix[0].size();
        vector<int> ans;
        int left = 0, right = n-1;
        int top = 0, bottom = m-1;
        
        while(left<=right && top<=bottom){
            // 左到右
            for(int i = left;i<=right;++i){
                ans.push_back(matrix[top][i]);
            }
            //上到下
            for(int i = top+1;i<=bottom;++i){
                ans.push_back(matrix[i][right]);
            }
            
            // 小心单行的情况
            //右到左
            if (top != bottom){
                for(int i = right-1; i>=left;--i){
                    ans.push_back(matrix[bottom][i]);
                }
            }
            // 下到上
            if (left != right){
                for(int i = bottom-1;i>top;--i){
                    ans.push_back(matrix[i][left]);
                }
            }
            top++;
            bottom--;
            left++;
            right--;
        }
        return ans;
    }

队列&栈

包含min函数的栈

用了个辅助栈，保存当前最小值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
class Solution {
public:
    stack<int> st;
    stack<int> aux_st;
    void push(int value) {
        st.push(value);
        if(aux_st.empty() || aux_st.top() >= value){
            aux_st.push(value);   //保存当前最小值
        }
    }
    void pop() {
        int temp = st.top();
        st.pop();
        if(temp == aux_st.top()){
            aux_st.pop();
        }
    }
    int top() {
        return st.top();
    }
    int min() {
        return aux_st.top();
    }
};

栈的压入、弹出序列

判断出栈序列有没有可能是入栈序列的对应序列。

入栈1,2,3,4,5

出栈4,5,3,2,1

首先1入辅助栈，此时栈顶1≠4，继续入栈2

此时栈顶2≠4，继续入栈3

此时栈顶3≠4，继续入栈4

此时栈顶4＝4，出栈4，弹出序列向后一位，此时为5，,辅助栈里面是1,2,3

此时栈顶3≠5，继续入栈5

此时栈顶5=5，出栈5,弹出序列向后一位，此时为3，,辅助栈里面是1,2,3

….

依次执行，最后辅助栈为空。如果不为空说明弹出序列不是该栈的弹出顺序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
bool IsPopOrder(vector<int> pushV,vector<int> popV) {
        stack<int> aux_st;
        size_t n = pushV.size();
        size_t j = 0;
        for(size_t i = 0;i < n;++i){
            aux_st.push(pushV[i]);  // 当前值入辅助栈
            while((!aux_st.empty() && aux_st.top()==popV[j])){
                // 判断辅助栈当前顶部能否弹出和当前出栈序列对应的值
                aux_st.pop();
                ++j;  // 出栈序列后移一位
            }           
        }
        return aux_st.empty();
    }

搜索算法

字符串的排列

算法

字符串的排列

tag: 字符串 递归

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
vector<string> Permutation(string str) {
        vector<string> vec;
        do{
            vec.push_back(str);
        }while(next_permutation(str.begin(), str.end()));
        return vec;
    }

// string内没有重复字母
class Solution {
public:
    vector<string> ans;
    void permu_unique(string& str, int index){
        if(index == str.size()){
            ans.emplace_back(str);
        }
        for(int i = index;i<str.size();++i){
            swap(str[i], str[index]);
            permu_unique(str, index + 1);
            swap(str[i], str[index]);
        }
    }
    vector<string> Permutation(string str) {
        permu_unique(str, 0);
        return ans;
    }
};

// string内有重复字母
class Solution {
public:
    vector<string> ans;
    vector<int> visited; // 记录重复字母
    
    // index代表选择的字母个数
    void permu(string& str, int index, string& temp){
        if(index == str.size()){
            ans.emplace_back(temp);
        }
        for(int i = 0; i<str.size();++i){
            if(visited[i] || (i>0 && !visited[i-1] && str[i-1] == str[i])){
                //!visited[i-1] && str[i-1] == str[i]
                //这句代表，前一个是没访问过的状态，并且当前字母等于前一个字母
                // 说明  前一个字母已经遍历完了，把状态重置为0，才来这个字母
                // 而两个字母相同，所以不该对当前字母再进行搜索
                continue;
            }
            // 选当前
            temp.push_back(str[i]);
            // 标记为已用
            visited[i] = 1;
            permu(str, index+1, temp);
            // 回退
            temp.pop_back();
            visited[i]=0;
        }
    }
    
    vector<string> Permutation(string str) {
        sort(str.begin(),str.end());
        string temp = "";
        visited.resize(str.size(),0);
        permu(str, 0, temp);
        return ans;
    }
};


其他算法

数组中出现次数超过一半的数字

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
//  题目输入保证有解，不需要在进行验证
int MoreThanHalfNum_Solution(vector<int> numbers) {
        int cnt = 0;
        int num = -1;
        for(auto &a : numbers){
            if(cnt == 0){  // 还没选数字
                num  = a;
                ++cnt;
            }else{
                if(a == num){  // 相同则给当前数字投一票
                    ++cnt;
                }else{
                    --cnt;  // 不同则减去一票
                }
            }
        }
        return num;
    }